Find the
(i) lengths of major axes,
(ii) coordinates of the vertices,
(iii) coordinates of the foci,
(iv) eccentricity, and
(v) length of the latus rectum of each of the following ellipses.
$9 x^{2}+y^{2}=36$
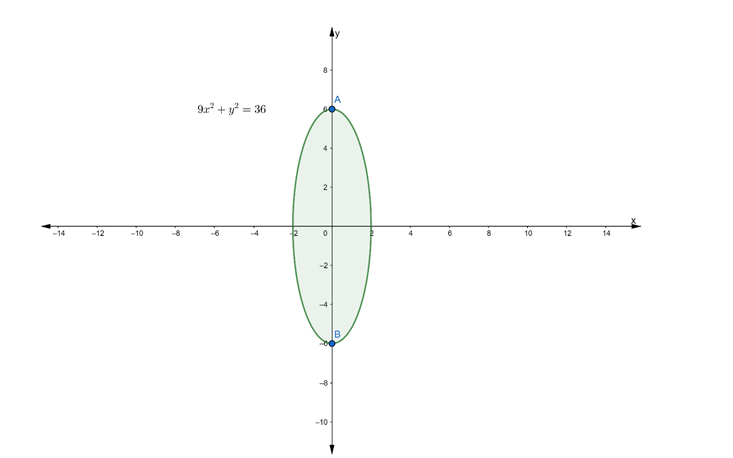
Given
$9 x^{2}+y^{2}=36$
Divide by 36 to both the sides, we get
$\frac{9}{36} x^{2}+\frac{1}{36} y^{2}=1$
$\frac{x^{2}}{4}+\frac{y^{2}}{36}=1$ …(i)
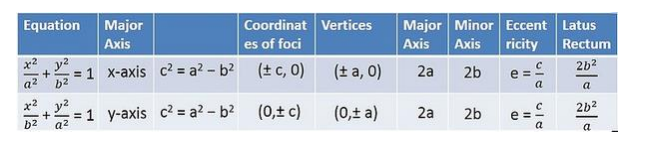
Since, 4 < 36
So, above equation is of the form,
$\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1$ …(ii)
Comparing eq. (i) and (ii), we get
$a^{2}=36$ and $b^{2}=4$
$\Rightarrow a=\sqrt{36}$ and $b=\sqrt{4}$
$\Rightarrow a=6$ and $b=2$
(i) To find: Length of major axes
Clearly, $a $\therefore$ Length of major axes $=2 \mathrm{a}$ $=2 \times 6$ $=12$ units (ii) To find: Coordinates of the Vertices Clearly, a > b $\therefore$ Coordinate of vertices $=(0, a)$ and $(0,-a)$ $=(0,6)$ and $(0,-6)$ (iii) To find: Coordinates of the foci We know that, Coordinates of foci $=(0, \pm c)$ where $c^{2}=a^{2}-b^{2}$ So, firstly we find the value of c $c^{2}=a^{2}-b^{2}$ $=36-4$ $c^{2}=32$ $c=\sqrt{32} \ldots(l)$ $\therefore$ Coordinates of foci $=(0, \pm \sqrt{32})$ (iv) To find: Eccentricity We know that, Eccentricity $=\frac{\mathrm{c}}{\mathrm{a}}$ $\Rightarrow \mathrm{e}=\frac{\sqrt{32}}{6}[$ from $(\mathrm{I})]$ (v) To find: Length of the Latus Rectum We know that, Length of Latus Rectum $=\frac{2 b^{2}}{a}$ $=\frac{2 \times(2)^{2}}{6}$ $=\frac{8}{6}$ $=\frac{4}{3}$
