Find the value of

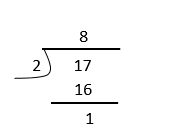
To find: Value of $\cos \frac{17 n}{2}$

$\cos \frac{17 \pi}{2}=\cos \left(8 \pi+\frac{1}{2} \pi\right)$

$=\cos \left(4 \times(2 \pi)+\frac{1}{2} \pi\right)$

Value of $\cos x$ repeats after an interval of $2 \pi$, hence ignoring $4 \times(2 \pi)$

$=\cos \left(\frac{1}{2} \pi\right)$

$=\cos \left(\frac{1}{2} \times 180^{\circ}\right)$

$=\cos 90^{\circ}$

$=0\left[\because \cos 90^{\circ}=1\right]$