Find the values of x in each of the following

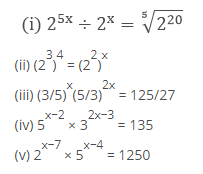
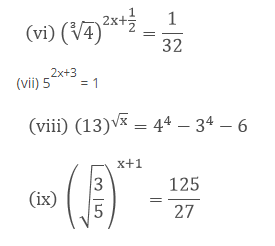
We have

$2^{5 x} \div 2^{x}=\sqrt[5]{\left(2^{20}\right)}$

$=\frac{2^{5 x}}{2^{x}}=\left(2^{20}\right)^{\frac{1}{5}}$

$=2^{5 x-x}=2^{20 \times \frac{1}{5}}$

$=2^{4 x}=2^{4}$

= 4x = 4 [On equating exponent]

x = 1

Hence the value of x is 1

(ii) $\left(2^{3}\right)^{4}=\left(2^{2}\right)^{x}$

We have

$\left(2^{3}\right)^{4}=\left(2^{2}\right)^{x}$

$=2^{3 \times 4}=2^{2 \times x}$

12 = 2x

2x = 12 [On equating exponents]

x = 6

Hence the value of x is 6

(iii) $(3 / 5)^{x}(5 / 3)^{2 x}=125 / 27$

We have

$(3 / 5)^{x}(5 / 3)^{2 x}=125 / 27$

$\Rightarrow \frac{(3)^{x}}{(5)^{x}} \frac{(5)^{2 x}}{(3)^{2 x}}=\frac{5^{3}}{3^{3}}$

$\Rightarrow 5^{2 x-x} / 3^{2 x-x}=5^{3} / 3^{3}$

$\Rightarrow 5^{x} / 3^{x}=5^{3} / 3^{3}$

$\Rightarrow(5 / 3)^{x}=(5 / 3)^{3}$

x = 3 [on equating exponents]

Hence the value of x is 3

(iv) $5^{x-2} \times 3^{2 x-3}=135$

We have,

$5^{x-2} \times 3^{2 x-3}=135$

$\Rightarrow 5^{x-2} \times 3^{2 x-3}=5 \times 27$

$\Rightarrow 5^{x-2} \times 3^{2 x-3}=5^{1} \times 3^{3}$

⇒ x − 2 = 1, 2x − 3 = 3 [On equating exponents]

⇒ x = 2 + 1, 2x = 3 + 3

⇒ x = 3, 2x = 6

⇒ x = 3

Hence the value of x is 3

(v) $2^{x-7} \times 5^{x-4}=1250$

We have

$2^{x-7} \times 5^{x-4}=1250$

$\Rightarrow 2^{x-7} \times 5^{x-4}=2 \times 625$

$\Rightarrow 2^{x-7} \times 5^{x-4}=2 \times 5^{4}$

⇒ x − 7 = 1

⇒ x = 8, x − 4 = 4

⇒ x = 8

Hence the value of x is 8

(vi) $(\sqrt[3]{4})^{2 x+\frac{1}{2}}=\frac{1}{32}$

$\left(4^{\frac{1}{3}}\right)^{2 x+\frac{1}{2}}=\frac{1}{32}$

$(4)^{\frac{1}{3}\left(2 x+\frac{1}{2}\right)}=\frac{1}{32}$

$(4)^{\frac{1}{3}(2 x+12)}=\frac{1}{2^{5}}$

$(4)^{\frac{2}{3} x+\frac{1}{6}}=\frac{1}{2^{5}}$

$\left(2^{2}\right)^{\frac{2}{3} x+\frac{1}{6}}=\frac{1}{2^{5}}$

(2) $^{2\left(\frac{2}{3} x+\frac{1}{6}\right)}=\frac{1}{2^{5}}$

$(2)^{\frac{4}{3} x+\frac{2}{6}}=\frac{1}{2^{5}}$

$(2)^{\frac{4}{3} x+\frac{1}{3}}=2^{-5}$

$\frac{4}{3} x+\frac{1}{3}=-5$

4x + 1 = -15

4x = -15 - 1

4x = -16

x = (-16)/4

x = - 4

Hence the value of x is 4

(vii) $5^{2 x+3}=1$

$5^{2 x+3}=1 \times 5^{0}$

2x + 3 = 0 [By equating exponents]

2x = −3

x = −3/2

Hence the value of x is −3/2

(viii) $(13)^{\sqrt{x}}=4^{4}-3^{4}-6$

$(13)^{\sqrt{x}}=256-81-6$

$(13)^{\sqrt{x}}=256-87$

$(13)^{\sqrt{x}}=169$

$(13)^{\sqrt{x}}=13^{2}$

$\sqrt{x}=2$ [By equating exponents]

$(\sqrt{x})^{2}=(2)^{2}$

x = 4

Hence the value of x is 4

(ix) $\left(\sqrt{\frac{3}{5}}\right)^{x+1}=\frac{125}{27}$

$\left(\sqrt{\frac{3}{5}}\right)^{x+1}=\frac{5^{3}}{3^{3}}$

$\left(\sqrt{\frac{3}{5}}\right)^{x+1}=\left(\frac{5}{3}\right)^{3}$

$\left(\sqrt{\frac{3}{5}}\right)^{x+1}=\left(\frac{3}{5}\right)^{-3}$

$\left(\frac{3}{5}\right)^{\frac{1}{2}(x+1)}=\left(\frac{3}{5}\right)^{-3}$

$\frac{1}{2}(x+1)=-3$

x + 1 = - 6

x = - 6 - 1

x = -7

Hence the value of x is 7