Find the volume of the largest right circular cone that can be cut out of a cube whose edge is 9 cm.
We have the following figure
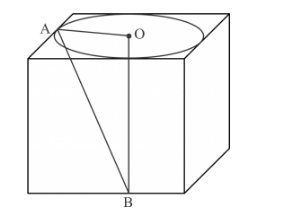
The length of each side of the cube is 9 cm. We have to find the volume of the largest right circular cone contained in the cube.
The diameter of the base circle is same as the length of the side of the cube. Thus, the diameter of the base circle of the right circular cone is 9 cm. Therefore, the radius of the base of the right
circular cone is $r=4.5 \mathrm{~cm}$.
From the right angled triangle $\triangle \mathrm{AOB}$ we have
h = 9 cm
Therefore, the volume of the solid right circular cone is
$V=\frac{1}{3} \pi r^{2} h$
$=\frac{1}{3} \times \frac{22}{7} \times(4.5)^{2} \times 9$
$=190.93$
Hence largest volume of cone is $190.93 \mathrm{~cm}^{3}$
