Find the zeros of each of the following quadratic polynomial and verify the relationship between the zeros and their coefficients:
Find the zeros of each of the following quadratic polynomial and verify the relationship between the zeros and their coefficients:
(i) $f(x)=x^{2}-2 x-8$
(ii) $g(s)=4 s^{2}-4 s+1$
(iii) $h(t)=t^{2}-15$
(iv) $6 x^{2}-3-7 x$
(v) $p(x)=x^{2}+2 \sqrt{2} x-6$
(vi) $q(x)=\sqrt{3} x^{2}+10 x+7 \sqrt{3}$
(vii) $f(x)=x^{2}-(\sqrt{3}+1) x+\sqrt{3}$
(viii) $g(x)=a\left(x^{2}+1\right)-x\left(a^{2}+1\right)$
(ix) $h(s)=2 s^{2}-(1+2 \sqrt{2}) s+\sqrt{2}$
(x) $f(v)=v^{2}+4 \sqrt{3} v-15$
(xi) $p(y)=y^{2}+\frac{3 \sqrt{5}}{2} y-5$
(xii) $q(y)=7 y^{2}-\frac{11}{3} y-\frac{2}{3}$
(i) We have,
f(x) = x2 − 2x − 8
f(x) = x2 + 2x − 4x − 8
f(x) = x (x + 2) − 4(x + 2)
f(x) = (x + 2) (x − 4)
The zeros of f(x) are given by
f(x) = 0
x2 − 2x − 8 = 0
(x + 2) (x − 4) = 0
x + 2 = 0
x = −2
Or
x − 4 = 0
x = 4
Thus, the zeros of f(x) = x2 − 2x − 8 are α = −2 and β = 4
Now,
Sum of the zeros $=\alpha+\beta$
$=(-2)+4$
$=-2+4$
$=2$
and
$=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
$=-\left(\frac{-2}{1}\right)$
= 2
Therefore, sum of the zeros $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
Product of the zeros $=\alpha \beta$
$=-2 \times 4$
$=-8$
and
$=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
$=\frac{-8}{1}$
$=-8$
Therefore,
Product of the zeros $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
Hence, the relation-ship between the zeros and coefficient are verified.
(ii) Given $g(s)=4 s^{2}-4 s+1$
When have,
g(s) = 4s2 − 4s + 1
g(s) = 4s2 − 2s − 2s + 1
g(s) = 2s (2s − 1) − 1(2s − 1)
g(s) = (2s − 1) (2s − 1)
The zeros of g(s) are given by
$g(s)=0$
$4 s^{2}-4 s+1=0$
$(2 s-1)(2 s-1)=0$
$(2 s-1)=0$
$2 s=+1$
$s=\frac{+1}{2}$
Or
$(2 s-1)=0$
$2 s=1$
$s=\frac{1}{2}$
Thus, the zeros of $g(x)=4 s^{2}-4 s+1$ are
$\alpha=\frac{1}{2}$ and $\beta=\frac{1}{2}$
Now, sum of the zeros $=\alpha+\beta$
$=\frac{1}{2}+\frac{1}{2}$
$=\frac{1+1}{2}$
$=\frac{2}{2}$
= 1
and
$\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
$=-\frac{-4}{4}$
= 1
Therefore, sum of the zeros $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
$=\frac{1}{2} \times \frac{1}{2}$
$=\frac{1}{4}$
and $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
$=\frac{1}{4}$
Therefore, the product of the zeros $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
Hence, the relation-ship between the zeros and coefficient are verified.
(iii) Given $h(t)=t^{2}-15$
We have,
$h(t)=t^{2}-15$
$h(t)=(t)^{2}-(\sqrt{15})^{2}$
$h(t)=(t+\sqrt{15})(t-\sqrt{15})$
The zeros of $h(t)$ are given by
$h(t)=0$
$(t-\sqrt{15})(t+\sqrt{15})=0$
$(t-\sqrt{15})=0$
$t=\sqrt{15}$
Or
$(t+\sqrt{15})=0$
$t=-\sqrt{15}$
Hence, the zeros of $h(t)$ are $\alpha=\sqrt{15}$ and $\beta=-\sqrt{15}$.
Now,
Sum of the zeros $=\alpha+\beta$
$=\sqrt{15}+(-\sqrt{15})$
$=\sqrt{15}-\sqrt{15}$
$=0$
and $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
$=\frac{0}{1}$
= 0
Therefore, sum of the zeros $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
also,
Product of the zeros $=\alpha \beta$
$=\sqrt{15} \times-\sqrt{15}$
$=-15$
and,
Constant term
$\overline{\text { Coefficient of } x^{2}}$
$=\frac{-15}{1}$
$=-15$
Therefore, the product of the zeros $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
Hence, The relationship between the zeros and coefficient are verified.
(iv) Given $f(x)=6 x^{2}-3-7 x$
We have, $f(x)=6 x^{2}-7 x-3$
$f(x)=6 x^{2}-9 x+2 x-3$
$f(x)=3 x(2 x-3)+1(2 x-3)$
$f(x)=(3 x+1)(2 x-3)$
The zeros of $f(x)$ are given by
$f(x)=0$
$6 x^{2}-7 x-3=0$
$(3 x+1)(2 x-3)=0$
$3 x=-1$
$x=\frac{-1}{3}$
Or
$2 x-3=0$
$2 x=3$
$x=\frac{3}{2}$
Thus, the zeros of $f(x)=6 x^{2}-7 x-3$ are $\alpha=\frac{-1}{3}$ and $\beta=\frac{3}{2}$.
Now,
Sum of the zeros $=\alpha+\beta$
$=\frac{-1}{3}+\frac{3}{2}$
$=\frac{-1 \times 2}{3 \times 2}+\frac{3 \times 3}{2 \times 3}$
$=\frac{-2}{6}+\frac{9}{6}$
$=\frac{-2+9}{6}$
$=\frac{7}{6}$
and, $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
$=\frac{-(-7)}{6}$
$=\frac{7}{6}$
Therefore, sum of the zeros $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
Product of the zeros = α × β
$=\frac{-1}{2}$
and, $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
$=\frac{-3}{6}$
$=\frac{-1}{2}$
Product of zeros $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
Hence, the relation between the zeros and its coefficient are verified.
(v) Given $p(x)=x^{2}+2 \sqrt{2} x-6$
We have,
$p(x)=x^{2}+2 \sqrt{2} x-6$
$p(x)=x^{2}+3 \sqrt{2} x-\sqrt{2} x-6$
$p(x)=x(x+3 \sqrt{2})-\sqrt{2}(x+3 \sqrt{2})$
$p(x)=(x-\sqrt{2})(x+3 \sqrt{2})$
The zeros of $p(x)$ are given by
$p(x)=0$
$p(x)=x^{2}+2 \sqrt{2} x-6$
$x^{2}+2 \sqrt{2} x-6=0$
$(x-\sqrt{2})(x+3 \sqrt{2})=0$
$(x-\sqrt{2})=0$
$x=\sqrt{2}$
Or
$(x+3 \sqrt{2})=0$
$x=-3 \sqrt{2}$
Thus, The zeros of $p(x)=x^{2}+2 \sqrt{2} x-6$ are $\alpha=\sqrt{2}$ and $\beta=-3 \sqrt{2}$
Now,
Sum of the zeros $=\alpha+\beta$
$=\sqrt{2}-3 \sqrt{2}$
$=+\sqrt{2}(1-3)$
$=\sqrt{2}(-2)$
$=-2 \sqrt{2}$
and
$=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
$=\frac{-2 \sqrt{2}}{1}$
$=-2 \sqrt{2}$
Therefore, Sum of the zeros $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
Product of the zeros $=\alpha \times \beta$
$=\sqrt{2} \times-3 \sqrt{2}$
$=-3 \times 2$
$=-6$
and
$\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
$=\frac{-6}{1}$
$=-6$
Therefore, The product of the zeros $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
Hence, the relation-ship between the zeros and coefficient are verified.
(vi) Given $q(x)=\sqrt{3} x^{2}+10 x+7 \sqrt{3}$
We have, $q(x)=\sqrt{3} x^{2}+10 x+7 \sqrt{3}$
$q(x)=\sqrt{3} x^{2}+3 x+7 x+7 \sqrt{3}$
$q(x)=\sqrt{3} x^{2}+\sqrt{3} \times \sqrt{3} \times x+7 x+7 \sqrt{3}$
$q(x)=\sqrt{3} x(x+\sqrt{3})+7(x+\sqrt{3})$
$q(x)=(x+\sqrt{3})(\sqrt{3} x+7)$
The zeros of g(x) are given by
$g(x)=0$
$\sqrt{3} x^{2}+10 x+7 \sqrt{3}=0$
$(x+\sqrt{3})(\sqrt{3} x+7)=0$
$x+\sqrt{3}=0$
$x=-\sqrt{3}$
Or
$\sqrt{3}+7=0$
$\sqrt{3} x=-7$
$x=\frac{-7}{\sqrt{3}}$
Thus, the zeros of $q(x)=\sqrt{3} x^{2}+10 x+7 \sqrt{3}$ are $\alpha=-\sqrt{3}$ and $\beta=\frac{-7}{\sqrt{3}}$.
Now,
Sum of the zeros $=\alpha+\beta$
$=-\sqrt{3}+\frac{-7}{\sqrt{3}}$
$=\frac{-\sqrt{3} \times \sqrt{3}}{1 \times \sqrt{3}}+\frac{-7}{\sqrt{3}}$
$=\frac{-3}{\sqrt{3}}+\frac{-7}{\sqrt{3}}$
$=\frac{-3-7}{\sqrt{3}}$
$=\frac{-10}{\sqrt{3}}$
and $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
$=\frac{-(+10)}{\sqrt{3}}$
$=\frac{-10}{\sqrt{3}}$
Therefore, sum of the zeros $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
Product of zeros $=\alpha \times \beta$
$=+7$
and $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
$=7$
Therefore, the product of the zeros $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
Hence, the relation-ship between the zeros and coefficient are verified.
(vii) Given $f(x)=x^{2}-(\sqrt{3}+1) x+\sqrt{3}$
$f(x)=x^{2}-\sqrt{3} x-1 x+\sqrt{3}$
$f(x)=x(x-\sqrt{3})-1(x-\sqrt{3})$
$f(x)=(x-1)(x-\sqrt{3})$
The zeros of ƒ(x) are given by
$f(x)=0$
$x^{2}-(\sqrt{3}+1) x+\sqrt{3}=0$
$(x-1)(x-\sqrt{3})=0$
$(x-1)=0$
$x=0+1$
$x=1$
Or
$x-\sqrt{3}=0$
$x=0+\sqrt{3}$
$x=\sqrt{3}$
Thus, the zeros of $x^{2}-(\sqrt{3}+1) x+\sqrt{3}$ are $\alpha=1$ and $\beta=\sqrt{3}$
Now,
Sum of zeros $=\alpha+\beta$
$=1+\sqrt{3}$
$=1+\sqrt{3}$
and
$=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
$=-\frac{-(\sqrt{3}+1)}{1}$
$=\frac{+(\sqrt{3}+1)}{1}$
Therefore, sum of the zeros $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
Product of the zeros $=\alpha \beta$
$=1 \times \sqrt{3}$
$=\sqrt{3}$
And
$=\frac{\text { Constant term }}{\text { Con } 2}$
$=\frac{\sqrt{3}}{1}$
$=\sqrt{3}$
Product of zeros $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
Hence, the relation-ship between the zeros and coefficient are verified.
(viii) Given $g(x)=a\left(x^{2}+1\right)-x\left(a^{2}+1\right)$
$g(x)=a x^{2}-x a^{2}+a-x$
$g(x)=x a(x-a)-1(x-a)$
$g(x)=(x a-1)(x-a)$
The zeros of g(x) are given by
$g(x)=0$
$a x^{2}-\left(a^{2}+1\right) x+a=0$
$x a-1=0$
$x a=1$
$x=\frac{1}{a}$
Or
$x-a=0$
$x=a$
Thus, the zeros of $g(x)=a x^{2}-\left(a^{2}+1\right) x+a$ are
$\alpha=\frac{1}{a}$ and $\beta=a$
Sum of the zeros $=\alpha+\beta$
$=\frac{1}{a}+a$
$=\frac{1}{a}+\frac{a \times a}{1 \times a}$
$=\frac{1+a^{2}}{a}$
and, $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
$=\frac{-\left(a^{2}+1\right)}{a}$
$=\frac{a^{2}+1}{a}$
Product of the zeros $=\alpha \times \beta$
$=\frac{1}{a} \times a$
= 1
And, $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
$=\frac{a}{a}$
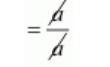
= 1
Therefore,
Product of the zeros $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
Hence, the relation-ship between the zeros and coefficient are verified.
(ix) $h(s)=2 s^{2}-(1+2 \sqrt{2}) s+\sqrt{2}$
$h(s)=2 s^{2}-s-2 \sqrt{2} s+\sqrt{2}$
$h(s)=s(2 s-1)-\sqrt{2}(2 s-1)$
h(s)=(2 s-1)(s-\sqrt{2})
The zeros of h(s) are given by
h(s) = 0
$2 s^{2}-(1+2 \sqrt{2}) s+\sqrt{2}=0$
$(2 s-1)(s-\sqrt{2})=0$
$(2 s-1)=0$ or $(s-\sqrt{2})=0$
$s=\frac{1}{2}$ or $s=\sqrt{2}$
Thus, the zeros of $h(s)=(2 s-1)(s-\sqrt{2})$ are $\alpha=\frac{1}{2}$ and $\beta=\sqrt{2}$.
Now,
Sum of the zeros $=\alpha+\beta$
$=\frac{1}{2}+\sqrt{2}$
and
$\frac{-\text { Coefficient of } s}{\text { Coefficient of } s^{2}}$
$=\frac{1+2 \sqrt{2}}{2}$
$=\frac{1}{2}+\sqrt{2}$
Therefore, sum of the zeros $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
Product of the zeros $=\alpha \beta$
$=\frac{1}{2} \times \sqrt{2}=\frac{1}{\sqrt{2}}$
and
$\frac{\text { Constant term }}{\text { Coefficient of } s^{2}}$
$=\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}$
Therefore,
Product of the zeros $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
Hence, the relation-ship between the zeros and coefficient are verified.
(x) $f(v)=v^{2}+4 \sqrt{3} v-15$
$f(v)=v^{2}+5 \sqrt{3} v-\sqrt{3} v-15$
$=v^{2}-\sqrt{3} v+5 \sqrt{3} v-15$
$=v(v-\sqrt{3})+5 \sqrt{3}(v-\sqrt{3})$
$=(v-\sqrt{3})(v+5 \sqrt{3})$
The zeros of f(v) are given by
f(v) = 0
$v^{2}+4 \sqrt{3} v-15=0$
$(v+5 \sqrt{3})(v-\sqrt{3})=0$
$(v-\sqrt{3})=0$ or $(v+5 \sqrt{3})=0$
$v=\sqrt{3}$ or $v=-5 \sqrt{3}$
Thus, the zeros of $f(v)=(v-\sqrt{3})(v+5 \sqrt{3})$ are $\alpha=\sqrt{3}$ and $\beta=-5 \sqrt{3}$.
Now,
Sum of the zeros $=\alpha+\beta$
$=\sqrt{3}-5 \sqrt{3}=-4 \sqrt{3}$
and
$\frac{\text { - Coefficient of } v}{\text { Coefficient of } v^{2}}$
$=\frac{-4 \sqrt{3}}{1}=-4 \sqrt{3}$
Therefore, sum of the zeros $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
Product of the zeros $=\alpha \beta$
$=\sqrt{3} \times(-5 \sqrt{3})=-15$
and
$\frac{\text { Constant term }}{\text { Coefficient of } v^{2}}$
$=\frac{-15}{1}=-15$
Therefore,
Product of the zeros $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
Hence, the relation-ship between the zeros and coefficient are verified.
(xi) $p(y)=y^{2}+\frac{3 \sqrt{5}}{2} y-5$
$p(y)=\frac{1}{2}\left(2 y^{2}+4 \sqrt{5} y-\sqrt{5} y-10\right)$
$=\frac{1}{2}[2 y(y+2 \sqrt{5})-\sqrt{5}(y+2 \sqrt{5})]$
$=\frac{1}{2}[(2 y-\sqrt{5})(y+2 \sqrt{5})]$
The zeros are given by p(y) = 0.
Thus, the zeros of $p(y)=\frac{1}{2}(2 y-\sqrt{5})(y+2 \sqrt{5})$ are $\alpha=\frac{\sqrt{5}}{2}$ and $\beta=-2 \sqrt{5}$.
Now,
Sum of the zeros $=\alpha+\beta$
$=\frac{\sqrt{5}}{2}-2 \sqrt{5}=\frac{\sqrt{5}-4 \sqrt{5}}{2}=\frac{-3 \sqrt{5}}{2}$
and
$\frac{\text { - Coefficient of } y}{\text { Coefficient of } y^{2}}$
$=\frac{\frac{-3 \sqrt{5}}{2}}{1}=\frac{-3 \sqrt{5}}{2}$
Therefore, sum of the zeros $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
Product of the zeros $=\alpha \beta$
$=\frac{\sqrt{5}}{2} \times-2 \sqrt{5}$
$=-5$
and
$\frac{\text { Constant term }}{\text { Coefficient of } y^{2}}$
$=\frac{-5}{1}=-5$
Therefore,
Product of the zeros $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
Hence, the relation-ship between the zeros and coefficient are verified.
(xii) $q(y)=7 y^{2}-\frac{11}{3} y-\frac{2}{3}$
$q(y)=\frac{1}{3}\left(21 y^{2}-11 y-2\right)$
$=\frac{1}{3}\left(21 y^{2}-14 y+3 y-2\right)$
$=\frac{1}{3}[7 y(3 y-2)+1(3 y-2)]$
$=\frac{1}{3}[(7 y+1)(3 y-2)]$
The zeros are given by q(y) = 0.
Thus, the zeros of $q(y)=\frac{1}{3}(7 y+1)(3 y-2)$ are $\alpha=\frac{-1}{7}$ and $\beta=\frac{2}{3}$.
Now,
Thus, the zeros of $q(y)=\frac{1}{3}(7 y+1)(3 y-2)$ are $\alpha=\frac{-1}{7}$ and $\beta=\frac{2}{3}$.
Now,
Sum of the zeros $=\alpha+\beta$
$=\frac{-1}{7}+\frac{2}{3}$
$=\frac{11}{21}$
and
$\frac{-\text { Coefficient of } y}{\text { Coefficient of } y^{2}}$
$=\frac{-\left(-\frac{11}{3}\right)}{7}=\frac{11}{21}$
Therefore, sum of the zeros $=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$
Product of the zeros $=\alpha \beta$
$=\frac{-1}{7} \times \frac{2}{3}$
$=\frac{-2}{21}$
and
$\frac{\text { Constant term }}{\text { Coefficient of } y^{2}}$
$=\frac{\frac{-2}{3}}{7}$
$=\frac{-2}{21}$
Therefore,
Product of the zeros $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$
Hence, the relation-ship between the zeros and coefficient are verified.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
