Find two positive numbers x and y such that their sum is

Let one number be x. Then, the other number is y = (35 − x).

Let $P(x)=x^{2} y^{5}$. Then, we have:

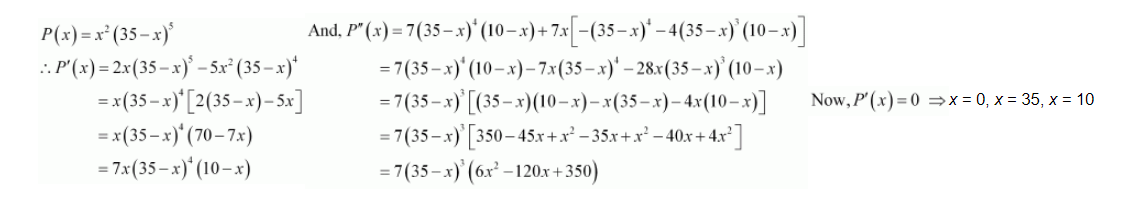
When $x=35, f^{\prime}(x)=f(x)=0$ and $y=35-35=0$. This will make the product $x^{2} y^{5}$ equal to 0 .

When $x=0 \quad y=35-0=35$ and the nroduct $x^{2} v^{2}$ will be 0

∴ x = 0 and x = 35 cannot be the possible values of x.

When x = 10, we have:

$\begin{aligned} P^{\prime \prime}(x) &=7(35-10)^{3}(6 \times 100-120 \times 10+350) \\ &=7(25)^{3}(-250)<0 \end{aligned}$

$\therefore$ By second derivative test, $P(x)$ will be the maximum when $x=10$ and $y=35-10=25$.

Hence, the required numbers are 10 and 25 .