For any sets A and B, prove that:

Solution:

Two sets are shown with the following Venn Diagram

The yellow region is denoted by 1.

Blue region is denoted by 2.

The common region is denoted by 3.

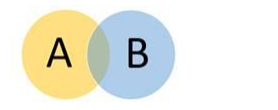
(i) A - B denotes region 1

B denotes region (2+3)

So their intersection is a : set

$\Rightarrow(A-B)^{\cap} B=\varnothing$

(ii) B - A denotes region 2

A denotes region (1+3)

So their union denotes region (1+2+3) which is the union of A and B

$\Rightarrow \mathrm{A}^{\mathrm{U}}(\mathrm{B}-\mathrm{A})=\mathrm{A}^{\mathrm{U}} \mathrm{B}$

(iii) A - B denotes region 1

$\mathrm{A}^{U} \mathrm{~B}$ denotes region 3

Their union denotes region $(1+3)$ which is set $A \Rightarrow(A-B) \cup_{(A} \cap_{B)}=A$

(iv) $\mathrm{A} \cup \mathrm{B}$ denotes region $(1+2+3)$

$(\mathrm{AUB})-\mathrm{B}$ denotes region $(1+2+3)-(2+3)=1 \mathrm{~A}-\mathrm{B}$ denotes region $1 \Rightarrow\left(\mathrm{A}^{\mathrm{U}} \mathrm{B}\right)-\mathrm{B}=\mathrm{A}-\mathrm{B}$

(v) Wrong question