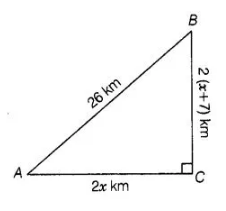
For going to a city B from city A there is a route

Given, AC ⊥ CB, km,CB = 2(x + 7) km and AB = 26 km

On drawing the figure, we get the right angled Δ ACB right angled at C.

Now, In ΔACB, by Pythagoras theorem,

$A B^{2}=A C^{2}+B C^{2}$

$\Rightarrow \quad(26)^{2}=(2 x)^{2}+\{2(x+7)\}^{2}$

$\Rightarrow \quad 676=4 x^{2}+4\left(x^{2}+49+14 x\right)$

$\Rightarrow \quad 676=4 x^{2}+4 x^{2}+196+56 x$

$\Rightarrow \quad 676=8 x^{2}+56 x+196$

$\Rightarrow \quad 8 x^{2}+56 x-480=0$

On dividing by 8 , we get $x^{2}+7 x-60=0$

$\Rightarrow \quad x^{2}+12 x-5 x-60=0$

$\Rightarrow \quad x(x+12)-5(x+12)=0$

$\Rightarrow \quad(x+12)(x-5)=0$

$\therefore \quad x=-12, x=5$

Since, distance cannot be negative.

$\therefore \quad x=5 \quad[\because x \neq-12]$ $[\because x \neq-12]$

Now, $A C=2 x=10 \mathrm{~km}$

and $\quad B C=2(x+7)=2(5+7)=24 \mathrm{~km}$

The distance covered to reach city $B$ from city A via city C

$=A C+B C$

$=10+24$

$=34 \mathrm{~km}$

Distance covered to reach city $B$ from city $A$ after the construction of the highway

$=B A=26 \mathrm{~km}$

Hence, the required saved distance is 34 – 26  i.e., 8 km.