For what value of k, −4 is a zero of the polynomial x2 − x − (2k + 2)?

We know that if $x=\alpha$ is zero polynomial then $x-2$ is a factor of $f(x)$

Since $-4$ is zero of $f(x)$

Therefore $x+4$ is a factor of $f(x)$

Now, we divide $f(x)=x^{2}-x-(2 k+2)$ by $g(x)=x+4$ to find the value of $k$

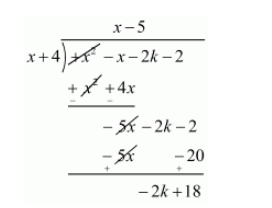
Now, Remainder $=0$

$-2 k+18=0$

$-2 k=-18$

$k=\frac{-18}{-2}$

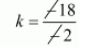
$k=9$

Hence, the value of $k$ is 9