Question.
Form the pair of linear equations in the following problems, and find their solutions graphi cally
(i) 10 students of class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
(ii) 5 pencils and 7 pens together cost ` 50, whereas 7 pencils and 5 pens together cost 46.
Find the cost of one pencil and that of one pen.
Form the pair of linear equations in the following problems, and find their solutions graphi cally
(i) 10 students of class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
(ii) 5 pencils and 7 pens together cost ` 50, whereas 7 pencils and 5 pens together cost 46.
Find the cost of one pencil and that of one pen.
Solution:
(i) Let the number of boys be x and the number of girls be y.
According to the given conditions
$x+y=10$ and $y=x+4$
We get the required pair of linear equations as
$x+y-10=0, x-y+4=0$
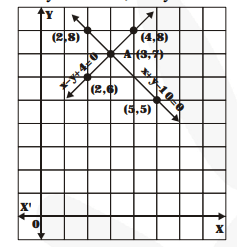
Graphical Solution
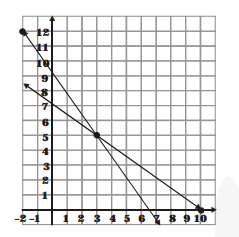
$x+y-10=0$...(1)
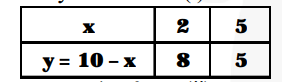
$x-y+4=0 \quad \ldots$...(ii)
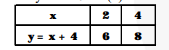
From the graph, we have : x = 3, y = 7 common solution of the two linear equations.
Hence, the number of boys = 3 and the number of girls = 7.
(ii) Let the cost of 1 pencil be Rs $x$ and cost of 1 pen be Rs. $y$.
$5 x+7 y=50$
$7 x+5 y=46$
$7 x+5 y=46$
5x + 7 y = 50° 7x + 5x = 46
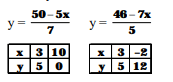
From the graph we have x = 3, y = 5.
Hence, cost of one pencil = Rs.3 and cost of
one pen = Rs.5
(i) Let the number of boys be x and the number of girls be y.
According to the given conditions
$x+y=10$ and $y=x+4$
We get the required pair of linear equations as
$x+y-10=0, x-y+4=0$
Graphical Solution
$x+y-10=0$...(1)
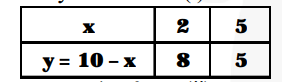
$x-y+4=0 \quad \ldots$...(ii)
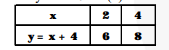
From the graph, we have : x = 3, y = 7 common solution of the two linear equations.
Hence, the number of boys = 3 and the number of girls = 7.
(ii) Let the cost of 1 pencil be Rs $x$ and cost of 1 pen be Rs. $y$.
$5 x+7 y=50$
$7 x+5 y=46$
$7 x+5 y=46$
5x + 7 y = 50° 7x + 5x = 46
From the graph we have x = 3, y = 5.
Hence, cost of one pencil = Rs.3 and cost of
one pen = Rs.5