Question.
Formulate the following problems as a pair of linear equations, and hence find their solutions:
(i) Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.
(ii) 2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.
(iii)Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Formulate the following problems as a pair of linear equations, and hence find their solutions:
(i) Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.
(ii) 2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.
(iii)Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Solution:
(i) Speed of Ritu in still water = x km/hr
Speed of current = y km/hr
Then speed downstream = (x + y) km/hr
speed upstream = (x – y) km/hr
$\frac{20}{x+y}=2$ and $\frac{4}{x-y}=2$
$\Rightarrow x+y=10$ ..(i)
$x-y=2$ ..(ii)
From (i) and (ii)
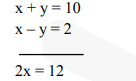
From (i)
$6+y=10$
$y=4$
So speed of Ritu = 6 km/hr and speed of current = 4 km/hr
(ii) Let 1 woman finish the work in x days and let 1 man finish the work in y days
Work of 1 woman in 1 day $=\frac{\mathbf{1}}{\mathbf{x}}$
Work of 1 man in 1 day $=\frac{\mathbf{1}}{\mathbf{y}}$
Work of 2 women and 5 men in one day
$=\frac{2}{x}+\frac{5}{y}=\frac{5 x+2 y}{x y}$
The number of days required for complete work $=\frac{\mathbf{x y}}{\mathbf{5 x}+\mathbf{2 y}}$
We are given that $\frac{\mathbf{x y}}{\mathbf{5 x}+\mathbf{2 y}}=4$
Similarly, in second case $\frac{\mathbf{x y}}{\mathbf{6 x}+\mathbf{3 y}}=\mathbf{3}$
$x y=4(5 x+2 y)$ ...(i)
$x y=3(6 x+3 y)$ ..(ii)
By solving, we get
$x y=20 x+8 y$
$x y=18 x+9 y$
$\Rightarrow \frac{20}{y}+\frac{8}{x}=1$ ...(iii)
$\frac{18}{y}+\frac{9}{x}=1$ ...(iv)
Putting $\frac{\mathbf{1}}{\mathbf{y}}=\mathrm{u}, \frac{\mathbf{1}}{\mathbf{x}}=\mathrm{v}$
$20 u+8 v=1$ ...(v)
$18 u+9 v=1$ ...(vi)
Multiply (v) by 9 and (vi) by 10
180u + 72v = 9
180u + 90v = 10
On subtracting, we get
$18 v=1 v=1 / 18$ and $u=1 / 36$
As $u=\frac{1}{\mathbf{3 6}}=\frac{1}{\mathbf{y}} \Rightarrow y=36$ days
and $v=\frac{1}{18}=\frac{1}{x} \Rightarrow x=18$ days
(iii) Let the speed of train be x km/hr and the speed of bus be y km/hr
So, $\frac{\mathbf{6 0}}{\mathbf{x}}+\frac{\mathbf{2 4 0}}{\mathbf{y}}=4$ ..(i)
$\frac{100}{x}+\frac{200}{y}=\frac{25}{6}$ ...(ii)
Let $\frac{\mathbf{1}}{\mathbf{x}}=\mathrm{u}, \quad \frac{\mathbf{1}}{\mathbf{y}}=\mathrm{v}$
$60 u+240 v=4$ ...(iii)
$100 \mathrm{u}+200 \mathrm{v}=\frac{\mathbf{2 5}}{\mathbf{6}}$ ...(iv)
Solving (iii) and (iv), we get
$u=\frac{1}{\mathbf{6 0}}, \quad v=\frac{1}{\mathbf{8 0}}$
So, $\frac{1}{x}=\frac{1}{60} \quad$ and $\quad \frac{1}{y}=\frac{1}{80}$
$\therefore \quad x=60 \mathrm{~km} / \mathrm{hr}$ and $y=80 \mathrm{~km} / \mathrm{hr}$
(i) Speed of Ritu in still water = x km/hr
Speed of current = y km/hr
Then speed downstream = (x + y) km/hr
speed upstream = (x – y) km/hr
$\frac{20}{x+y}=2$ and $\frac{4}{x-y}=2$
$\Rightarrow x+y=10$ ..(i)
$x-y=2$ ..(ii)
From (i) and (ii)
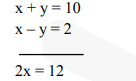
From (i)
$6+y=10$
$y=4$
So speed of Ritu = 6 km/hr and speed of current = 4 km/hr
(ii) Let 1 woman finish the work in x days and let 1 man finish the work in y days
Work of 1 woman in 1 day $=\frac{\mathbf{1}}{\mathbf{x}}$
Work of 1 man in 1 day $=\frac{\mathbf{1}}{\mathbf{y}}$
Work of 2 women and 5 men in one day
$=\frac{2}{x}+\frac{5}{y}=\frac{5 x+2 y}{x y}$
The number of days required for complete work $=\frac{\mathbf{x y}}{\mathbf{5 x}+\mathbf{2 y}}$
We are given that $\frac{\mathbf{x y}}{\mathbf{5 x}+\mathbf{2 y}}=4$
Similarly, in second case $\frac{\mathbf{x y}}{\mathbf{6 x}+\mathbf{3 y}}=\mathbf{3}$
$x y=4(5 x+2 y)$ ...(i)
$x y=3(6 x+3 y)$ ..(ii)
By solving, we get
$x y=20 x+8 y$
$x y=18 x+9 y$
$\Rightarrow \frac{20}{y}+\frac{8}{x}=1$ ...(iii)
$\frac{18}{y}+\frac{9}{x}=1$ ...(iv)
Putting $\frac{\mathbf{1}}{\mathbf{y}}=\mathrm{u}, \frac{\mathbf{1}}{\mathbf{x}}=\mathrm{v}$
$20 u+8 v=1$ ...(v)
$18 u+9 v=1$ ...(vi)
Multiply (v) by 9 and (vi) by 10
180u + 72v = 9
180u + 90v = 10
On subtracting, we get
$18 v=1 v=1 / 18$ and $u=1 / 36$
As $u=\frac{1}{\mathbf{3 6}}=\frac{1}{\mathbf{y}} \Rightarrow y=36$ days
and $v=\frac{1}{18}=\frac{1}{x} \Rightarrow x=18$ days
(iii) Let the speed of train be x km/hr and the speed of bus be y km/hr
So, $\frac{\mathbf{6 0}}{\mathbf{x}}+\frac{\mathbf{2 4 0}}{\mathbf{y}}=4$ ..(i)
$\frac{100}{x}+\frac{200}{y}=\frac{25}{6}$ ...(ii)
Let $\frac{\mathbf{1}}{\mathbf{x}}=\mathrm{u}, \quad \frac{\mathbf{1}}{\mathbf{y}}=\mathrm{v}$
$60 u+240 v=4$ ...(iii)
$100 \mathrm{u}+200 \mathrm{v}=\frac{\mathbf{2 5}}{\mathbf{6}}$ ...(iv)
Solving (iii) and (iv), we get
$u=\frac{1}{\mathbf{6 0}}, \quad v=\frac{1}{\mathbf{8 0}}$
So, $\frac{1}{x}=\frac{1}{60} \quad$ and $\quad \frac{1}{y}=\frac{1}{80}$
$\therefore \quad x=60 \mathrm{~km} / \mathrm{hr}$ and $y=80 \mathrm{~km} / \mathrm{hr}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
