Question:
Four equal circles, each of radius a units, touch each other. Show that the area between them is $\left(\frac{6}{7} a^{2}\right)$ sq units.
Solution:
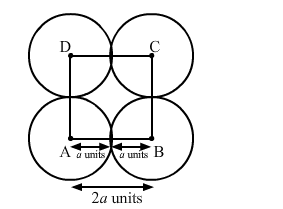
When four circles touch each other, their centres form the vertices of a square. The sides of the square are 2a units.
Area of the square $=(2 a)^{2}=4 a^{2}$ sq. units
Area occupied by the four sectors
$=4 \times \frac{90}{260} \times \pi \times a^{2}$
$=\pi a^{2}$ sq. units
Area between the circles = Area of the square
$=\left(4-\frac{22}{7}\right) a^{2}$
$=\frac{6}{7} a^{2}$ sq. units