From a circular piece of cardboard of radius 3 cm two sectors of 90° have been cut off.

It is very clear that if we cut two sectors of $90^{\circ}$ then we will be left with a semi-circle without diameter.

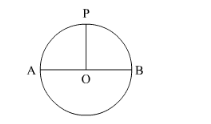
Look at the figure. If we cut sectors OPA and OPB then we will get curve AB.

Therefore, the required perimeter will be length of the curve AB.

Now we will calculate the perimeter of the remaining curve AB as shown below.

$\therefore$ Perimeter $=\pi r$

$\therefore$ Perimeter $=\frac{22}{7} \times 3$

$\therefore$ Perimeter $=\frac{66}{7}$

$\therefore$ Perimeter $=9.428$

Therefore, perimeter of the remaining portion is $9.428 \mathrm{~cm}$.