From a point on a bridge across a river the angles of depression of the banks on opposite side of the river are 30°

Let $B D$ be the width of river. And the angle of depression of the bank on opposite side of the river are $30^{\circ}$ and $45^{\circ}$ respectively. It is given that $A C=30 \mathrm{~m}$. Let $B C=x$ and $C D=y$. And $\angle A B C=30^{\circ}$, $\angle A D C=45^{\circ}$.

Here we have to find the width of river.

We have the following figure

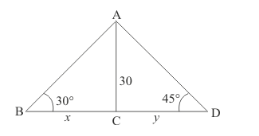
So we use trigonometric ratios.

In a triangle,

$\Rightarrow \quad \tan 30^{\circ}=\frac{A C}{B C}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{30}{x}$

$\Rightarrow \quad x=30 \sqrt{3}$

Again in a triangle,

$\Rightarrow \quad \tan 45^{\circ}=\frac{A C}{C D}$

$\Rightarrow \quad 1=\frac{30}{y}$

$\Rightarrow \quad y=30$

So width of river is:

$x+y=30 \sqrt{3}+30$

$x+y=30(\sqrt{3}+1)$

Hence the width of river is $30(\sqrt{3}+1) \mathrm{m}$.