From a point on the ground the angles of elevation of the bottom and top of a

Let be the building of height m and  the transmission tower of height  meter.

Again let the angle of elevation of the bottom and top of tower at the point  is 45° and 60° respectively.

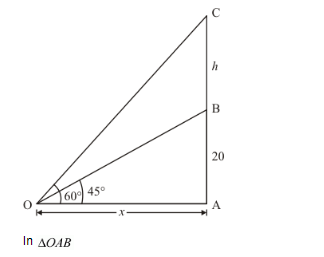
$\Rightarrow \quad \tan 45^{\circ}=\frac{A B}{O A}$

$\Rightarrow \quad 1=\frac{20}{x}$

$\Rightarrow \quad x=20$

Again in $\triangle O A C$

$\Rightarrow \quad \tan 60^{\circ}=\frac{A C}{O A}$

$\Rightarrow \quad \sqrt{3}=\frac{h+20}{x}$

$\Rightarrow \quad \sqrt{3} x=h+20$

$\Rightarrow \quad 20 \sqrt{3}=h+20$

$\Rightarrow \quad h=20 \sqrt{3}-20$

$\Rightarrow \quad h=20(\sqrt{3}-1)$

Hence the height of tower is $20(\sqrt{3}-1) \mathrm{m}$.