From a point on the ground the angles of elevation of the bottom and top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively.

PQ = 20 m is the height of the building. 

Let PR = h metres be the height of the transmission tower. P is the bottom and R is the top of the transmission tower.

$\angle \mathrm{POQ}=45^{\circ}$ and $\angle \mathrm{ROQ}=60^{\circ}$

From $\Delta \mathrm{OPQ}$,

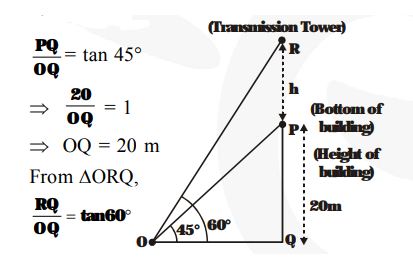
$\Rightarrow \frac{\mathbf{2 0}+\mathbf{h}}{\mathbf{2 0}}=\sqrt{\mathbf{3}}$

$(\because \mathrm{RQ}=\mathrm{PQ}+\mathrm{PR}=20+\mathrm{h}$ metres and $\mathrm{OQ}$

$=20$ metres $)$

$\Rightarrow 1+\frac{\mathbf{h}}{\mathbf{2 0}}=\sqrt{\mathbf{3}} \Rightarrow \frac{\mathbf{h}}{\mathbf{2 0}}=(\sqrt{\mathbf{3}}-\mathbf{1})$

$\Rightarrow \mathrm{h}=20(\sqrt{\mathbf{3}}-\mathbf{1}) \mathrm{m}$