From a point P which is at a distance of 13 cm

(a) Firstly, draw a circle of radius 5 cm having centre O. P is a point at a distance of 13 cm from O. A pair of tangents PQ and PR are drawn.

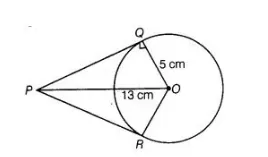
Thus, quadrilateral POOR is formed.

$\because \quad \quad O Q \perp Q P$ [since, AP is a tangent line]

In right angled $\triangle P Q O, \quad O P^{2}=O Q^{2}+Q P^{2}$

$\Rightarrow \quad 13^{2}=5^{2}+Q P^{2}$

$\Rightarrow \quad Q P^{2}=169-25=144$

$\Rightarrow \quad Q P=12 \mathrm{~cm}$

Now, area of $\Delta O Q P=\frac{1}{2} \times Q P \times Q O$

$=\frac{1}{2} \times 12 \times 5=30 \mathrm{~cm}^{2}$

$\therefore \quad$ Area of quadrilateral $Q O R P=2 \triangle O Q P$

$=2 \times 30=60 \mathrm{~cm}^{2}$