From a solid cube of side 7 cm,

Given that, side of a solid cube (a) = 7 cm

Height of conical cavity i.e., cone, h = 7 cm

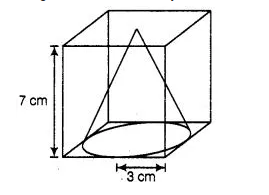
Since, the height of conical cavity and the side of cube is equal that means the conical cavity fit vertically in the cube.

Radius of conical cavity i.e., cone, r = 3 cm

⇒                                                        Diameter = 2 x r = 2 x 3= 6 cm

Since, the diameter is less than the side of a cube that means the base of a conical cavity is not fit inhorizontal face of cube.

Now, volume of cube $=(\text { side })^{3}=a^{3}=(7)^{3}=343 \mathrm{~cm}^{3}$

and volume of conical cavity $i . e .$, cone $=\frac{1}{3} \pi \times r^{2} \times h$

$=\frac{1}{3} \times \frac{22}{7} \times 3 \times 3 \times 7$

$=66 \mathrm{~cm}^{3}$

$\therefore$ Volume of remaining solid $=$ Volume of cube $-$ Volume of conical cavity

$=343-66=277 \mathrm{~cm}^{3}$

Hence, the required volume of solid is 277 cm³