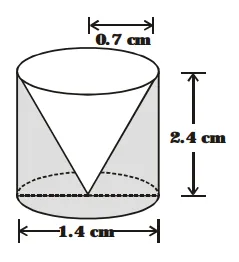
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm,

For cylinder part :

Height = 2.4 cm and diameter = 1.4 cm

$\Rightarrow$ Radius $(r)=0.7 \mathrm{~cm}$

$\therefore$ Total surface area of the cylindrical part

$=2 \times \frac{\mathbf{2 2}}{\mathbf{7}} \times \frac{\mathbf{7}}{\mathbf{1 0}}[2.4+0.7] \mathrm{cm}^{2}$

$=\frac{\mathbf{4 4}}{\mathbf{1 0}} \times 3.1 \mathrm{~cm}^{2}=\frac{\mathbf{4 4} \times \mathbf{3 1}}{\mathbf{1 0 0}}=\frac{\mathbf{1 3 6 4}}{\mathbf{1 0 0}} \mathbf{c m}^{2}$

For conical part :

Base radius (r) = 0.7 cm and height (h) = 2.4 cm

$\therefore$ Slant height $(\ell)=\sqrt{\mathbf{r}^{2}+\mathbf{h}^{2}}=\sqrt{(\mathbf{0 . 7})^{2}+(\mathbf{2 . 4})^{2}}$

$=\sqrt{\mathbf{0 . 4 9}+\mathbf{5 . 7 6}}=\sqrt{\mathbf{6 . 2 5}}=2.5 \mathrm{~cm}$

$\therefore$ Curved surface area of the conical part

=\pi \mathrm{r} \ell=\frac{\boldsymbol{2 2}}{\boldsymbol{7}} \times 0.7 \times 2.5 \mathrm{~cm}^{2}=\frac{\mathbf{5 5 0}}{\mathbf{1 0 0}} \mathrm{cm}^{2}

Base area of the conical part

$\pi r^{2}=\frac{22}{7} \times\left(\frac{7}{10}\right)^{2} \mathrm{~cm}^{2}=\frac{22 \times 7}{100} \mathrm{~cm}^{2}=\frac{154}{100} \mathrm{~cm}^{2}$

Total surface area of the remaining solid

$=[$ (Total surface area of cylinderical part) $+$ (Curved surface area of conical part) $-($ Base a of the conical part $)]=\left[\frac{1364}{100}+\frac{550}{100}-\frac{154}{100}\right] \mathrm{cm}^{2}$

$=\frac{\mathbf{1 7 6 0}}{\mathbf{1 0 0}} \mathrm{cm}^{2}=17.6 \mathrm{~cm}^{2}$

Hence, total surface area to the nearest $\mathrm{cm}^{2}$ is $18 \mathrm{~cm}^{2}$.