From a solid cylinder whose height is 8 cm and radius 6 cm, a conical cavity of height 8 cm and base radius 6 cm is hollowed out.

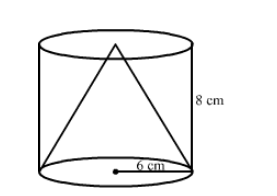
Volume of the solid left $=$ Volume of cylinder $-$ Volume of cone $=\pi r^{2} h-\frac{1}{3} \pi r^{2} h=\frac{2}{3} \times \frac{22}{7} \times 8 \times 6 \times 6=603.428 \mathrm{~cm}^{3}$

The slant length of the cone, $l=\sqrt{r^{2}+h^{2}}=\sqrt{36+64}=10 \mathrm{~cm}$

Total surface area of final solid = Area of base circle + Curved surface area of cylinder + Curved surface area of cone

$=\pi r^{2}+2 \pi r h+\pi r l=\pi r(r+2 h+l)=\frac{22}{7} \times 6 \times(6+16+10)=603.42 \mathrm{~cm}^{2}$