From a thin metallic piece in the shape of a trapezium ABCD in which AB || CD and ∠BCD = 90°, a quarter circle BFEC is removed. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of remaining (shaded) part of metal sheet.
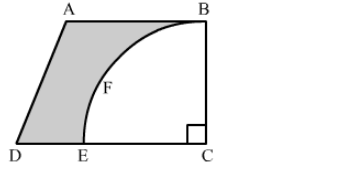
Since, BFEC is a quarter of a circle.
Hence, BC = EC = 3.5 cm
Now, DC = DE + EC = 2 + 3.5 = 5.5 cm
Area of shaded region = Area of the trapezium ABCD − Area of the quadrant BFEC
$=\frac{1}{2} \times(\mathrm{AB}+\mathrm{DC}) \times \mathrm{BC}-\frac{1}{4} \times \pi(\mathrm{EC})^{2}$
$=\frac{1}{2} \times(3.5+5.5) \times 3.5-\frac{1}{4} \times \frac{22}{7} \times(3.5)^{2}$
$=6.125 \mathrm{~cm}^{2}$
Hence, the area of the shaded region is 6.125 cm2 .
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
