From the prices of shares X and Y below, find out which is more stable in value:

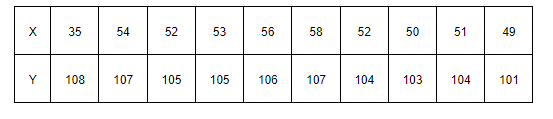
The prices of the shares X are

35, 54, 52, 53, 56, 58, 52, 50, 51, 49

Here, the number of observations, N = 10

$\therefore$ Mean, $\bar{x}=\frac{1}{N} \sum_{i=1}^{10} x_{i}=\frac{1}{10} \times 510=51$

The following table is obtained corresponding to shares X.

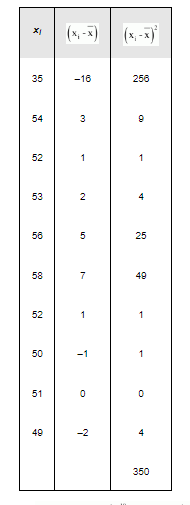
Variance $\left(\sigma_{1}^{2}\right)=\frac{1}{N} \sum_{i=1}^{10}(x i-\bar{x})^{2}=\frac{1}{10} \times 350=35$

$\therefore S \tan$ dard deviation $\left(\sigma_{1}\right)=\sqrt{35}=5.91$

C.V. $($ Shares $X)=\frac{\sigma_{1}}{x} \times 100=\frac{5.91}{51} \times 100=11.58$

The prices of share Y are

108, 107, 105, 105, 106, 107, 104, 103, 104, 101

$\therefore$ Mean, $\bar{y}=\frac{1}{N} \sum_{i=1}^{10} y_{i}=\frac{1}{10} \times 1050=105$

The following table is obtained corresponding to shares Y.

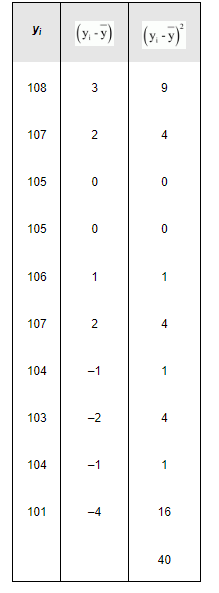
$\operatorname{Variance}\left(\sigma_{2}^{2}\right)=\frac{1}{N} \sum_{i=1}^{10}\left(y_{i}-\bar{y}\right)^{2}=\frac{1}{10} \times 40=4$

$\therefore$ Stan dard deviation $\left(\sigma_{2}\right)=\sqrt{4}=2$

$\therefore$ C.V.(Shares Y) $=\frac{\sigma_{2}}{\mathrm{y}} \times 100=\frac{2}{105} \times 100=1.9$

C.V. of prices of shares X is greater than the C.V. of prices of shares Y.

Thus, the prices of shares Y are more stable than the prices of shares X.