From the top of a 7 m high building,

Let PQ = h metres be the height of the cable tower.

AB = 7 metres is the height of the bulding 

$\angle \mathrm{PAR}=60^{\circ}$ is the angle of elevation of the top of the cable tower from the top of the building.

$\angle \mathrm{RAQ}=45^{\circ}$ is the angle of depression of the foot of the cable tower from the top of the building. Then $\angle \mathrm{AQB}=45^{\circ}$.

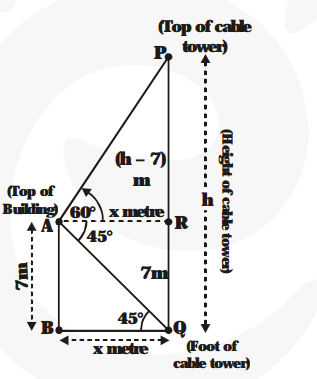
Now, $B Q=A R=x$ metres (say)

From $\Delta \mathrm{AQB}, \frac{\mathbf{A B}}{\mathbf{B Q}}=\tan 45^{\circ} \Rightarrow \frac{\mathbf{7}}{\mathbf{x}}=1 \Rightarrow \mathrm{x}=7 \mathrm{~m}$

Now, from $\Delta$ PAR, $\frac{\mathbf{P R}}{\mathbf{A R}}=\tan 60^{\circ} \Rightarrow \frac{\mathbf{P Q}-\mathbf{Q R}}{\mathbf{x}}=\sqrt{\mathbf{3}}$

$\Rightarrow \frac{\mathbf{h}-\mathbf{7}}{\mathbf{x}}=\sqrt{\mathbf{3}} \Rightarrow \frac{\mathbf{h}-\mathbf{7}}{\mathbf{7}}=\sqrt{\mathbf{3}} \Rightarrow \mathrm{h}=7(\sqrt{\mathbf{3}}+\mathbf{1})$

Hence, the height of the cable tower is $7(\sqrt{3}+1)$ metre.