From the top of a building AB, 60 m high, the angles of depression of the top and bottom of

Let $A B$ be the building of height 60 and $C D$ be the lamp post of height $h$, an angle of depression of the top and bottom of vertical lamp post are $30^{\circ}$ and $60^{\circ}$ respectively. Let $A E=h, A C=x$ and $A C=E D$. It is also given $A B=60 \mathrm{~m}$. Then $B E=60-h$ And $\angle A C B=60^{\circ}, \angle B D E=30^{\circ}$

We have to find the following

(i) The horizontal distance between AB and CD

(ii) The height of lamp post

(iii) The difference between the heights of building and the lamp post

We have the corresponding figure as follows

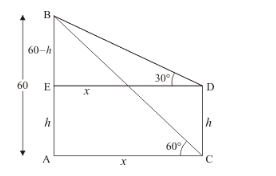
(i) So we use trigonometric ratios.

$\ln \Delta A B C$

$\Rightarrow \quad \tan 60^{\circ}=\frac{A B}{A C}$

$\Rightarrow \quad \sqrt{3}=\frac{60}{x}$

$\Rightarrow \quad x=\frac{60}{\sqrt{3}}$

$\Rightarrow \quad x=34.64$

Hence the distance between $A B$ and $C D$ is $34.64$

(ii) Again in 

$\Rightarrow \quad \tan 30^{\circ}=\frac{B E}{D E}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{60-h}{x}$

$\Rightarrow \quad \frac{60}{\sqrt{3}}=(60-h) \sqrt{3}$

$\Rightarrow \quad 60=180-3 h$

$\Rightarrow \quad 60=180-3 h$

$\Rightarrow \quad 3 h=120$

$\Rightarrow \quad 3 h=120$

$\Rightarrow \quad h=40$

Hence the height of lamp post is $40 \mathrm{~m}$.

(iii) Since BE $=60-h$

$\Rightarrow \quad B E=60-40$

$\Rightarrow \quad B E=20$

Hence the difference between height of building and lamp post is $20 \mathrm{~m}$.