From the top of a hill, the angles of depression of two consecutive kilometre stones due east are found to be 45° and 30°

Let PQ be the hill of height h km. Let R and S be two consecutive kilometre stones, so the distance between them is 1 km.
Let QR = x km.

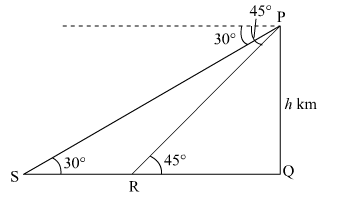
In $\Delta \mathrm{PQR}$,

$\tan 45^{\circ}=\frac{\mathrm{PQ}}{\mathrm{QR}}$

$\Rightarrow 1=\frac{h}{x}$

$\Rightarrow h=x \quad \ldots(i)$

In $\triangle \mathrm{PQS}$,

$\tan 30^{\circ}=\frac{\mathrm{PQ}}{\mathrm{QS}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{x+1}$

$\Rightarrow \sqrt{3} h=x+1 \quad \ldots$ (ii)

From equation (i) and (ii) we get,

$\sqrt{3} h=h+1$

$\Rightarrow h(\sqrt{3}-1)=1$

$\Rightarrow h=\frac{1}{\sqrt{3}-1}=\frac{\sqrt{3}+1}{(\sqrt{3}-1)(\sqrt{3}+1)}$

$\Rightarrow h=\frac{\sqrt{3}+1}{2}=\frac{2.73}{2}=1.365 \mathrm{~km}$

Hence, the height of the hill is 1.365 km.