From the top of a tower h m high,

Let the distance between two objects is x m,

and CD = y m.

Given that, ∠BAX = α = ∠ABD,              [alternate angle]

∠CAY = p = ∠ACD            [alternate angle]

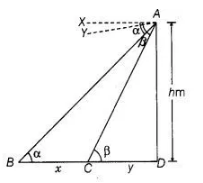
Now, in $\triangle A C D$,

$\tan \beta=\frac{A D}{C D}=\frac{h}{y}$

$\Rightarrow$ $y=\frac{h}{\tan \beta}$ .....(i)

and in $\triangle A B D$,

$\tan \alpha=\frac{A D}{B D} \quad \Rightarrow=\frac{A D}{B C+C D}$

$\Rightarrow$ $\tan \alpha=\frac{h}{x+y} \Rightarrow x+y=\frac{h}{\tan \alpha}$

$\Rightarrow$ $y=\frac{h}{\tan \alpha}-x$......(ii)

From Eqs. (i) and (ii), 

$\frac{h}{\tan \beta}=\frac{h}{\tan \alpha}-x$

$\therefore$ $x=\frac{h}{\tan \alpha}-\frac{h}{\tan \beta}$

$=h\left(\frac{1}{\tan \alpha}-\frac{1}{\tan \beta}\right)=h(\cot \alpha-\cot \beta)$ $\left[\because \cot \theta=\frac{1}{\tan \theta}\right]$'

which is the required distance between the two objects.

Hence proved.