Given examples of two functions f: N → N and g: N → N such that gof is onto but f is not onto.

Define f: N → N by,

f(x) = x + 1

And, g: N → N by,

$g(x)= \begin{cases}x-1 & \text { if } x>1 \\ 1 & \text { if } x=1\end{cases}$

We first show that g is not onto.

For this, consider element 1 in co-domain N. It is clear that this element is not an image of any of the elements in domain N.

∴ f is not onto.

Now, gof: N → N is defined by,

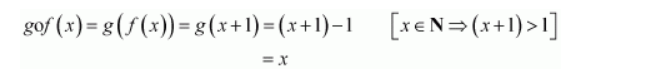
Then, it is clear that for $y \in \mathbf{N}$, there exists $x=y \in \mathbf{N}$ such that gof $(x)=y$.

Hence, gof is onto.