Graphically, solve the following pair

Given equations are $2 x+y=6$ and $2 x-y+2=0$

Table for equation $2 x+y=6$

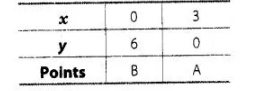
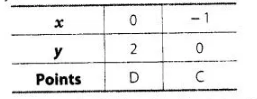
Table for equation $2 x-y+2=0$,

Let $A_{1}$ and $A_{2}$ represent the areas of $\triangle A C E$ and $\triangle B D E$, respectively.

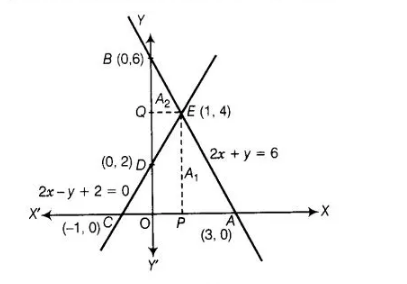
Now, $A_{1}=$ Area of $\triangle A C E=\frac{1}{2} \times A C \times P E$

$=\frac{1}{2} \times 4 \times 4=8$

and $A_{2}=$ Area of $\Delta B D E=\frac{1}{2} \times B D \times Q E$

$=\frac{1}{2} \times 4 \times 1=2$

$\therefore A_{1}: A_{2}=8: 2=4: 1$

Hence, the pair of equations intersect graphically at point $E(1,4), i . e ., x=1$ and $y=4$.