How many 6-digit numbers can be formed from the digits 0, 1, 3, 5, 7, 9 when no digit is repeated? How many of them are divisible by 10?
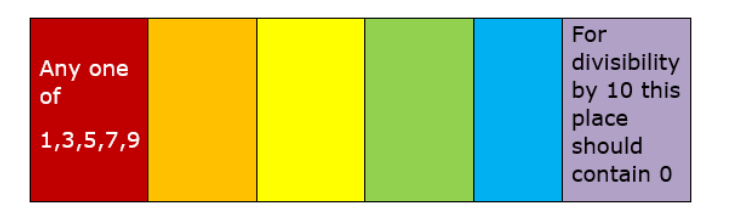
There are total 6 digits available ,for forming a 6 digit number, in 100000 's place only $1,3,5,7,9$ can be used( 0 not included because it will lead to formation of 2 digit number.)
In 10000 's place any of the remaining 5 digits can be used(even 0 can be used.)
In 1000's place any of the remaining 4 digits can be used.
In 100 's place any of the remaining 3 digits can be used.
In 10's place any of the remaining 2 digits can be used.
In one's place the remaining digit can be used.
So total number of 6 digit numbers possible $=5 \times 5 \times 4 \times 3 \times 2 \times 1=600$
For finding the number of 6 digit numbers divisible by 10 the one's place should contain 0 so possibilities $=5 \times 4 \times 3 \times 2 \times 1=120$