How many balls, each of radius I cm,

We are given a solid sphere with radius $R=8 \mathrm{~cm}$.

From this sphere we have to make spherical balls of radius $r=1 \mathrm{~cm}$.

Let the no. of balls that can be formed be $n$.

We know,

Volume of a sphere $=\frac{4}{3} \pi r^{3}$.

So, volume of the bigger solid sphere $=\frac{4}{3} \pi(8)^{3}$

Volume of one smaller spherical ball $=\frac{4}{3} \pi(1)^{3}$

We know, the volume of the solid sphere should be equal to the sum of the volumes of the n spherical balls formed.

So, using (a) and (b), we get,

$\Rightarrow n \times \frac{4}{3} \pi(1)^{3}=\frac{4}{3} \pi(8)^{3}$

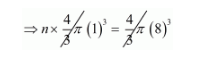
Therefore, $n=(8)^{3}$

$n=512$

Hence, the no. of balls of radius $r=1$ that can be formed out of solid sphere of radius $R=8$ is 512 .