How much paper of each shade is needed

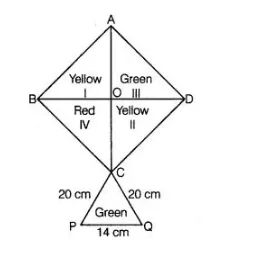
We know that, all the sides of a square are always equal.

i.e., $\quad A B=B C=C D=D A$

In $\triangle A C D$   $A C=44 \mathrm{~cm}, \angle D=90^{\circ}$

Using Pythagoras theorem in $\triangle A C D$,

$A C^{2}=A D^{2}+D C^{2}$

$\Rightarrow$ $44^{2}=A D^{2}+A D^{2}$ $[\because D C=A D]$

$\Rightarrow$ $2 A D^{2}=44 \times 44$

$\Rightarrow$ $A D^{2}=22 \times 44 \Rightarrow A D=\sqrt{22 \times 44}$

[taking positive square root because length is always positive]

$\Rightarrow$ $A D=\sqrt{2 \times 11 \times 4 \times 11}$

$\Rightarrow$ $A D=22 \sqrt{2} \mathrm{~cm}$

So, $A B=B C=C D=D A=22 \sqrt{2} \mathrm{~cm}$

$\therefore$ Area of square $A B C D=$ Side $\times$ Side $=22 \sqrt{2} \times 22 \sqrt{2}=968 \mathrm{~cm}^{2}$

$\therefore$ Area of the red portion $=\frac{968}{4}=242 \mathrm{~cm}^{2}$

[since, area of square is divided into four parts]

Now, area of the green portion $=\frac{968}{4}=242 \mathrm{~cm}^{2}$

Area of the yellow portion $=\frac{968}{2}=484 \mathrm{~cm}^{2}$

In $\triangle P C Q$, side $P C=a=20 \mathrm{~cm} C Q=b=20 \mathrm{~cm}$ and $P Q=c=14 \mathrm{~cm}$

$s=\frac{a+b+c}{2}=\frac{20+20+14}{2}=\frac{54}{2}=27 \mathrm{~cm}$

$\therefore$  Area of $\triangle P C Q=\sqrt{s(s-a)(s-b)(s-c)}$ [by Heron's formula]

$=\sqrt{27(27-20)(27-20)(27-14)}$

$=\sqrt{27 \times 7 \times 7 \times 13}=\sqrt{3 \times 3 \times 3 \times 7 \times 7 \times 13}$

$=21 \sqrt{39}=21 \times 6.24=131.04 \mathrm{~cm}^{2}$

$\therefore$ Total area of the green portion $=242+131.04)=373.04 \mathrm{~cm}^{2}$

Hence, the paper required for each shade to make a kite is red paper $242 \mathrm{~cm}^{2}$, yellow paper $484 \mathrm{~cm}^{2}$ and green paper $373.04 \mathrm{~cm}^{2}$.