Question.
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Solution:
Mid-point of the diagonal AC has x-coordinate
$=\frac{\mathbf{x}+\mathbf{1}}{\mathbf{2}}$ and $y$-coordinate $=\frac{\mathbf{6}+\mathbf{2}}{\mathbf{2}}=4$
i.e., $\left(\frac{\mathbf{x}+\mathbf{1}}{\mathbf{2}}, \mathbf{4}\right)$ is the mid-point of $\mathrm{AC}$.
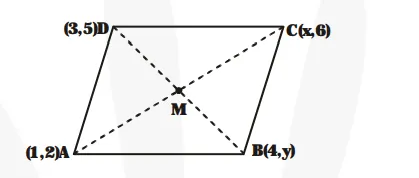
Similarly, mid-point of the diagonal BD is
$\left(\frac{\mathbf{4}+\mathbf{3}}{\mathbf{2}}, \frac{\mathbf{y}+\mathbf{5}}{\mathbf{2}}\right)$, i.e., $\left(\frac{\mathbf{7}}{\mathbf{2}}, \frac{\mathbf{y}+\mathbf{5}}{\mathbf{2}}\right)$
We know that the two diagonals AC and BD bisect each other at M. Therefore,
$\left(\frac{\mathbf{x}+\mathbf{1}}{\mathbf{2}}, \mathbf{4}\right)$ and $\left(\frac{\mathbf{7}}{\mathbf{2}}, \frac{\mathbf{y}+\mathbf{5}}{\mathbf{2}}\right)$. Coincide
$\Rightarrow \frac{\mathbf{x}+\mathbf{1}}{\mathbf{2}}=\frac{\mathbf{7}}{\mathbf{2}}$ and $\frac{\mathbf{y}+\mathbf{5}}{\mathbf{2}}=4$
$\Rightarrow x=6$ and $y=3$
Mid-point of the diagonal AC has x-coordinate
$=\frac{\mathbf{x}+\mathbf{1}}{\mathbf{2}}$ and $y$-coordinate $=\frac{\mathbf{6}+\mathbf{2}}{\mathbf{2}}=4$
i.e., $\left(\frac{\mathbf{x}+\mathbf{1}}{\mathbf{2}}, \mathbf{4}\right)$ is the mid-point of $\mathrm{AC}$.

Similarly, mid-point of the diagonal BD is
$\left(\frac{\mathbf{4}+\mathbf{3}}{\mathbf{2}}, \frac{\mathbf{y}+\mathbf{5}}{\mathbf{2}}\right)$, i.e., $\left(\frac{\mathbf{7}}{\mathbf{2}}, \frac{\mathbf{y}+\mathbf{5}}{\mathbf{2}}\right)$
We know that the two diagonals AC and BD bisect each other at M. Therefore,
$\left(\frac{\mathbf{x}+\mathbf{1}}{\mathbf{2}}, \mathbf{4}\right)$ and $\left(\frac{\mathbf{7}}{\mathbf{2}}, \frac{\mathbf{y}+\mathbf{5}}{\mathbf{2}}\right)$. Coincide
$\Rightarrow \frac{\mathbf{x}+\mathbf{1}}{\mathbf{2}}=\frac{\mathbf{7}}{\mathbf{2}}$ and $\frac{\mathbf{y}+\mathbf{5}}{\mathbf{2}}=4$
$\Rightarrow x=6$ and $y=3$
