If √2 is a zero of the cubic polynomial

Let f(x) = 6x3 + √2x2 -10x – 4√2 and given that. √2 is one of the zeroes of f(x) i.e.,(x – √2) is one of the factor of given cubic polynomial.

Now, using division algorithm,

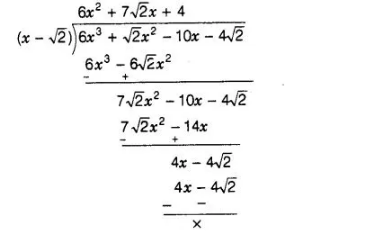
$\therefore \quad 6 x^{3}+\sqrt{2} x^{2}-10 x-4 \sqrt{2}=\left(6 x^{2}+7 \sqrt{2} x+4\right) \times(x-\sqrt{2})+0$

$[\because$ dividend $=$ divisor $x$ quotient $+$ remainder $]$

$=(x-\sqrt{2})\left(6 x^{2}+4 \sqrt{2} x+3 \sqrt{2} x+4\right)$

$=(x-\sqrt{2})\{\sqrt{2} x(3 \sqrt{2} x+4)+1(3 \sqrt{2} x+4)\}$

$=(x-\sqrt{2})\{(3 \sqrt{2} x+4)(\sqrt{2} x+1)\}$

$=(x-\sqrt{2})(\sqrt{2} x+1)(3 \sqrt{2} x+4)$

So, its other zeroes are $-\frac{1}{\sqrt{2}}$ and $-\frac{4}{3 \sqrt{2}}$.