Question:
If $27^{x}=\frac{9}{3^{x}}$, find $\mathrm{x}$
Solution:
We are given $27^{x}=\frac{9}{3^{x}}$. We have to find the value of $x$
Since $\left(3^{3}\right)^{x}=\frac{3^{2}}{3^{x}}$
By using the law of exponents $\frac{a^{m}}{a^{n}}=a^{m-n}$ we get,
$3^{3 x}=3^{2-x}$
On equating the exponents we get,
$\begin{aligned} 3 x &=2-x \\ 3 x+x &=2 \\ 4 x &=2 \\ x &=\frac{2}{4} \end{aligned}$
$x=\frac{1}{2}$
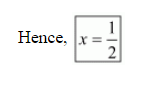
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
