Question.
If $3 \cot \mathrm{A}=4$, check whether $\frac{1-\tan ^{2} \mathbf{A}}{1+\tan ^{2} \mathbf{A}}=\cos ^{2} \mathrm{~A}-\sin ^{2} \mathrm{~A}$ or not.
If $3 \cot \mathrm{A}=4$, check whether $\frac{1-\tan ^{2} \mathbf{A}}{1+\tan ^{2} \mathbf{A}}=\cos ^{2} \mathrm{~A}-\sin ^{2} \mathrm{~A}$ or not.
Solution:
In figure,
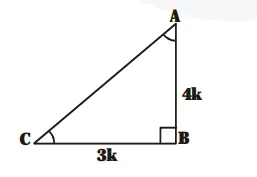
$3 \cot A=4$
$\Rightarrow \cot A=\frac{4}{3}$
$\Rightarrow \frac{A B}{B C}=\frac{4}{3}$
$\Rightarrow \mathrm{AB}=4 \mathrm{k}$ and $\mathrm{BC}=3 \mathrm{k}$
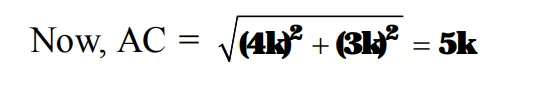
Then $\sin \mathrm{A}=\frac{\mathbf{B C}}{\mathbf{A C}}=\frac{\mathbf{3 k}}{\mathbf{5 k}}=\frac{\mathbf{3}}{\mathbf{5}}$,
$\cos A=\frac{A B}{A C}=\frac{4 k}{5 k}=\frac{4}{5}$
and $\tan \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{\mathbf{3 k}}{\mathbf{4 k}}=\frac{\mathbf{3}}{\mathbf{4}}$
$\operatorname{LHS}=\frac{1-\tan ^{2} A}{1+\tan ^{2} A}=\frac{1-\left(\frac{3}{4}\right)^{2}}{1+\left(\frac{3}{4}\right)^{2}}$
$=\frac{1-\frac{9}{16}}{1+\frac{9}{16}}=\frac{16-9}{16+9}=\frac{7}{25}$
$R H S=\cos ^{2} A-\sin ^{2} A=\left(\frac{4}{5}\right)^{2}-\left(\frac{3}{5}\right)^{2}$
$=\frac{16}{25}-\frac{9}{25}=\frac{7}{25}$
Therefore, LHS = RHS,
i.e., $\frac{1-\tan ^{2} \mathbf{A}}{1+\tan ^{2} \mathbf{A}}=\cos ^{2} \mathrm{~A}-\sin ^{2} \mathrm{~A}$
$\left(\because \operatorname{Eich} \sin =\frac{7}{25}\right)$
In figure,

$3 \cot A=4$
$\Rightarrow \cot A=\frac{4}{3}$
$\Rightarrow \frac{A B}{B C}=\frac{4}{3}$
$\Rightarrow \mathrm{AB}=4 \mathrm{k}$ and $\mathrm{BC}=3 \mathrm{k}$
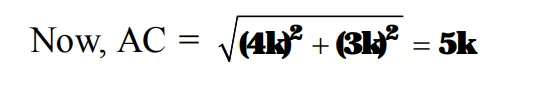
Then $\sin \mathrm{A}=\frac{\mathbf{B C}}{\mathbf{A C}}=\frac{\mathbf{3 k}}{\mathbf{5 k}}=\frac{\mathbf{3}}{\mathbf{5}}$,
$\cos A=\frac{A B}{A C}=\frac{4 k}{5 k}=\frac{4}{5}$
and $\tan \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{\mathbf{3 k}}{\mathbf{4 k}}=\frac{\mathbf{3}}{\mathbf{4}}$
$\operatorname{LHS}=\frac{1-\tan ^{2} A}{1+\tan ^{2} A}=\frac{1-\left(\frac{3}{4}\right)^{2}}{1+\left(\frac{3}{4}\right)^{2}}$
$=\frac{1-\frac{9}{16}}{1+\frac{9}{16}}=\frac{16-9}{16+9}=\frac{7}{25}$
$R H S=\cos ^{2} A-\sin ^{2} A=\left(\frac{4}{5}\right)^{2}-\left(\frac{3}{5}\right)^{2}$
$=\frac{16}{25}-\frac{9}{25}=\frac{7}{25}$
Therefore, LHS = RHS,
i.e., $\frac{1-\tan ^{2} \mathbf{A}}{1+\tan ^{2} \mathbf{A}}=\cos ^{2} \mathrm{~A}-\sin ^{2} \mathrm{~A}$
$\left(\because \operatorname{Eich} \sin =\frac{7}{25}\right)$
