If (- 4, 3) and (4, 3) are two vertices of an equilateral triangle,

Let the third vertex of an equilateral triangle be $(x, y)$. Let $A(-4,3), B(43)$ and $C(x, y)$.

We know that, in equilateral triangle the angle between two adjacent side is 60 and all three sides are equal.

$\therefore$ $A B=B C=C \cdot A$

$\Rightarrow$ $A B^{2}=B C^{2}=C A^{2}$ ...(i)

Now, taking first two parts.

$A B^{2}=B C^{2}$

$\Rightarrow \quad(4+4)^{2}+(3-3)^{2}=(x-4)^{2}+(y-3)^{2}$

$\Rightarrow \quad 64+0=x^{2}+16-8 x+y^{2}+9-6 y$

$\Rightarrow \quad x^{2}+y^{2}-8 x-6 y=39$

Now, taking first and third parts,

$A B^{2}=C A^{2}$

$\Rightarrow \quad(4+4)^{2}+(3-3)^{2}=(-4-x)^{2}+(3-y)^{2}$

$\Rightarrow \quad 64+0=16+x^{2}+8 x+9+y^{2}-6 y$

$\Rightarrow \quad x^{2}+y^{2}+8 x-6 y=39$...(iii)

On subtracting Eq. (ii) from Eq. (iii), we get

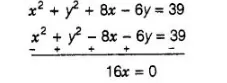
$\Rightarrow$ $x=0$

On subtracting Eq. (ii) from Eq. (iii), we get

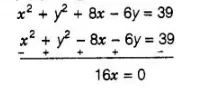
$\Rightarrow \quad x=0$

Now, put the value of $x$ in Eq. (ii), we get

$\Rightarrow \quad y^{2}-6 y-39=0$

$\therefore$ $y=\frac{6 \pm \sqrt{(-6)^{2}-4(1)(-39)}}{2 \times 1}$

$\left[\because\right.$ solution of $a x^{2}+b x+c=0$ is $\left.x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\right]$

$\Rightarrow$ $y=\frac{6 \pm \sqrt{36+156}}{2}$

$\Rightarrow$ $y=\frac{6 \pm \sqrt{192}}{2}$

$\Rightarrow$ $y=\frac{6 \pm 2 \sqrt{48}}{2}=3 \pm \sqrt{48}$

$\Rightarrow$ $y=3 \pm 4 \sqrt{3}$

$\Rightarrow \quad y=3+4 \sqrt{3}$ or $3-4 \sqrt{3}$

So, the points of third vertex are $(0,3+4 \sqrt{3})$ or $(3-4 \sqrt{3)}$

But given that, the origin lies in the interior of the $\triangle A B C$ and the $x$-coordinate of third vertex is zero. Then, $y$-coordinate of third vertex should be negative.

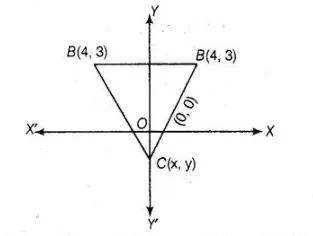
Hence, the required coordinate of third vertex, $C \equiv(0,3-4 \sqrt{3}) . \quad[\because c \equiv(0,3+4 \sqrt{3})]$