Question.
If $\mathrm{A}$ and $\mathrm{B}$ are $(-2,-2)$ and $(2,-4)$, respectively, find the coordinates of $\mathrm{P}$ such that $\mathrm{AP}=$ $\frac{\mathbf{3}}{\mathbf{7}} \mathrm{AB}$ and $\mathrm{P}$ lies on the line segment $\mathrm{AB}$.
If $\mathrm{A}$ and $\mathrm{B}$ are $(-2,-2)$ and $(2,-4)$, respectively, find the coordinates of $\mathrm{P}$ such that $\mathrm{AP}=$ $\frac{\mathbf{3}}{\mathbf{7}} \mathrm{AB}$ and $\mathrm{P}$ lies on the line segment $\mathrm{AB}$.
Solution:
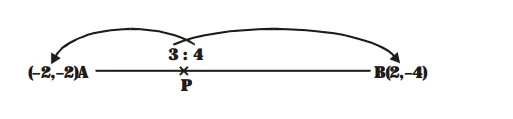
$\mathrm{AP}=\frac{3}{7} \mathrm{AB}$
$\mathrm{BP}=\mathrm{AB}-\mathrm{AP}=\mathrm{AB}-\frac{\mathbf{3}}{7} \mathrm{AB}=\frac{4}{7} \mathrm{AB}$
$\frac{A P}{B P}=\frac{\frac{3}{7} A B}{\frac{4}{7} A B}=\frac{3}{4}$
Thus, $\mathrm{P}$ divides $\mathrm{AB}$ in the ratio $3: 4$.
$x$-coordinate of $P=\frac{3 \times(2)+4 \times(-2)}{3+4}=-\frac{2}{7}$
$y$-coordinate of $P=\frac{3 \times(-4)+4 \times(-2)}{3+4}=-\frac{20}{7}$
Hence, the coordiantes of $P$ are $\left(-\frac{2}{7},-\frac{20}{7}\right)$

$\mathrm{AP}=\frac{3}{7} \mathrm{AB}$
$\mathrm{BP}=\mathrm{AB}-\mathrm{AP}=\mathrm{AB}-\frac{\mathbf{3}}{7} \mathrm{AB}=\frac{4}{7} \mathrm{AB}$
$\frac{A P}{B P}=\frac{\frac{3}{7} A B}{\frac{4}{7} A B}=\frac{3}{4}$
Thus, $\mathrm{P}$ divides $\mathrm{AB}$ in the ratio $3: 4$.
$x$-coordinate of $P=\frac{3 \times(2)+4 \times(-2)}{3+4}=-\frac{2}{7}$
$y$-coordinate of $P=\frac{3 \times(-4)+4 \times(-2)}{3+4}=-\frac{20}{7}$
Hence, the coordiantes of $P$ are $\left(-\frac{2}{7},-\frac{20}{7}\right)$
