. If A ⊂ B, prove that B’ ⊂ A’.

As $A \subset B$ the set $A$ is inside set $B$

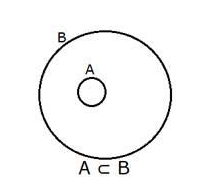
Hence $A \cup B=B$

Taking compliment

$\Rightarrow(A \cup B)^{\prime}=B .^{\prime}$

Using de-morgans law $(A \cup B)^{\prime}=A^{\prime} \cap B .^{\prime}$

$\Rightarrow A^{\prime} \cap B^{\prime}=B .^{\prime}$

$A^{\prime} \cap B^{\prime}=B^{\prime}$ means that the set $B^{\prime}$ is inside the set $A . .^{\prime}$

Representing in Venn diagram,

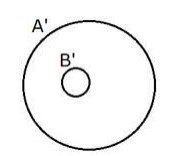
As seen from Venn diagram $B^{\prime} \subset A . '$

Hence proved