Question:
If a chord AB subtends an angle of 60∘ at the centre of a circle, then the angle between the tangents to the circle drawn from A and B isl to
(a) 30∘
(b) 60∘
(c) 90∘
(d) 120∘
Solution:
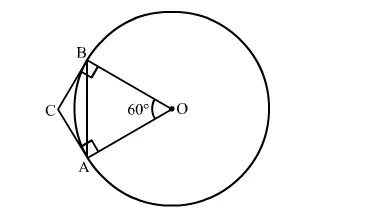
We know that the radius and tangent are perperpendular at their point of contact
∵∠OBC = ∠OAC = 90∘
Now, In quadrilateral ABOC
∠ACB + ∠OAC + ∠OBC + ∠AOB = 360∘ [Angle sum property of a quadrilateral]
⇒ ∠ACB + 90∘ + 90∘ + 60∘ = 360∘
⇒ ∠ACB + 240∘ = 360∘
⇒ ∠ACB = 120∘
Hence, the correct answer is option (d).
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.