If a line is drawn parallel to the base

Given ΔABC is an isosceles triangle such that AB = AC and also DE || SC.

To prove Quadrilateral BCDE is a cyclic quadrilateral.

Construction Draw a circle passes through the points B, C, D and E.

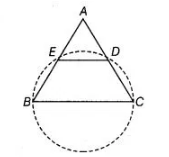
Proof in $\triangle A B C$,  [equal sides of an isosceles triangle]

$\Rightarrow$ $\angle A C B=\angle A B C$ $\ldots(1)$

[angles opposite to the equal sides are equal]

Since, $D E \| B C$

$\Rightarrow \quad \angle A D E=\angle A C B \quad$ [corresponding angles] ...(ii)

On adding both sides by $\angle E D C$ in Eq. (ii), we get

$\angle A D E+\angle E D C=\angle A C B+\angle E D C$

$\Rightarrow \quad 180^{\circ}=\angle A C B+\angle E D C$

[ $\angle A D E$ and $\angle E D C$ form linear pair aniom]

$\Rightarrow \quad \angle E D C+\angle A B C=180^{\circ} \quad$ [from Eq. (1)]

Hence, $B C D E$ is a cyclic quadrilateral, because sum of the opposite angles is $180^{\circ}$.