If a man standing on a plat form 3 m above

Solution:

False

From figure, we observe that, a man standing on a platform at point P, 3 m above the surface of a lake observes a cloud at point C. Let the height

of the cloud from the surface of the platform is h and angle of elevation of the cloud is θ1.

Now at same point P a man observes a cloud reflection in the lake at this time the height of reflection of cloud in lake is

(h + 3) because in lake platform height is also added to reflection of cloud.

So,angle of depression is different  in the lake from the angle of elevation of the cloud above the surface of a lake

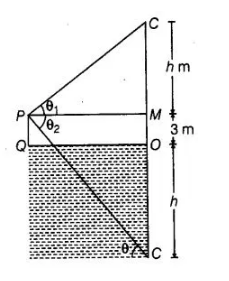
$\ln \triangle M P C_{1}$ $\tan \theta_{1}=\frac{C M}{P M}=\frac{h}{P M}$

$\Rightarrow$ $\frac{\tan \theta_{1}}{h}=\frac{1}{P M}$ $\ldots$ (i)

In $\Delta C P M$, $\tan \theta_{2}=\frac{C M}{P M}=\frac{O C+O M}{P M}=\frac{h+3}{P M}$

 $\Rightarrow$ $\frac{\tan \theta_{2}}{h+3}=\frac{1}{P M}$ ...(ii)

From Eqs. (i) and (ii),

$\frac{\tan \theta_{1}}{h}=\frac{\tan \theta_{2}}{h+3}$

$\Rightarrow$ $\tan \theta_{2}=\left(\frac{h+3}{h}\right) \tan \theta_{1}$

Hence, $\theta_{1} \neq \theta_{2}$

Alternate Method

False, we know that, if P is a point above the lake at a distance d, then the reflection of the point in the lake wouid be at the same distanced. Also,

the angle of elevation and depression from the surface of the lake is same.

Here, the man is standing on a platform 3 m above the surface, so its angle of elevation to the cloud and angle of depression to the reflection of

the cloud is not same.