If a number of circles touch a given

False

Given that PQ is any line segment and S1, S2, S3, S4,… circles are touch a line segment PQ at a point A. Let the centres of the circlesS1,S2, S3,

S4,… be C1 C2, C3, C4,… respectively.

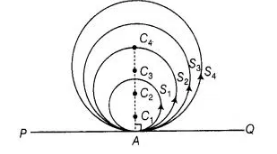
To prove centres of these circles lie on the perpendicular bisector PQ

Now, joining each centre of the circles to the point A on the line segment PQ by a line segment i.e., C1A, C2A, C3A, C4A… so on.

We know that, if we draw a line from the centre of a circle to its tangent line, then the line is always perpendicular to the tangent line. But it not

bisect the line segment PQ.

So,

Since, each circle is passing through a point A. Therefore, all the line segments

C1A, C2A, C3A, C4A…. so on are coincident.

So, centre of each circle lies on the perpendicular line of PQ but they do not lie on the perpendicular bisector of PQ.

Hence, a number of circles touch a given line segment PQ at a point A, then their centres lie