If a point $C$ lies between two points $A$ and $B$ such that $A C=B C$, then prove that $A C=\frac{1}{2} A B .$ Explain by drawing the figure.
Solution:
It is given that,
$\mathrm{AC}=\mathrm{BC}$
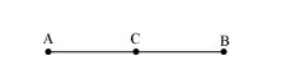
$\mathrm{AC}+\mathrm{AC}=\mathrm{BC}+\mathrm{AC}$ (Equals are added on both sides) $\ldots$ (1)
Here, $(\mathrm{BC}+\mathrm{AC})$ coincides with $\mathrm{AB}$. It is known that things which coincide with one another are equal to one another.
$\therefore \mathrm{BC}+\mathrm{AC}=\mathrm{AB} \ldots$(2)
It is also known that things which are equal to the same thing are equal to one another. Therefore, from equations (1) and (2), we obtain
$\mathrm{AC}+\mathrm{AC}=\mathrm{AB}$
$2 \mathrm{AC}=\mathrm{AB}$
$\therefore \mathrm{AC}=\frac{1}{2} \mathrm{AB}$
It is given that,
$\mathrm{AC}=\mathrm{BC}$

$\mathrm{AC}+\mathrm{AC}=\mathrm{BC}+\mathrm{AC}$ (Equals are added on both sides) $\ldots$ (1)
Here, $(\mathrm{BC}+\mathrm{AC})$ coincides with $\mathrm{AB}$. It is known that things which coincide with one another are equal to one another.
$\therefore \mathrm{BC}+\mathrm{AC}=\mathrm{AB} \ldots$(2)
It is also known that things which are equal to the same thing are equal to one another. Therefore, from equations (1) and (2), we obtain
$\mathrm{AC}+\mathrm{AC}=\mathrm{AB}$
$2 \mathrm{AC}=\mathrm{AB}$
$\therefore \mathrm{AC}=\frac{1}{2} \mathrm{AB}$
