If a young man rides his motorcycle at $40 \mathrm{~km}$ per hour, he has to spend $6 \mathrm{per} \mathrm{km}$ on petrol and if he rides it at $50 \mathrm{~km}$ hour, the petrol cost rises to 10 per $\mathrm{km}$. He has 500 to spend on petrol and wishes to find the maximum distance he can travel within one hour. Formulate the data in the form of inequation and draw a graph representing the solution of these inequations.
Let the distance covered with speed $40 \mathrm{~km} / \mathrm{hr}=\mathrm{x} \mathrm{km}$
And the distance covered with speed $50 \mathrm{~km} / \mathrm{hr}=\mathrm{y} \mathrm{km}$
We know that,
Time $=\frac{\text { Distance }}{\text { Speed }}$
Therefore, maximum speed covered within one hour is
$\frac{x}{40}+\frac{y}{50} \leq 1$
Thus, according to equation,
Maximum speed covered,$Z_{\max }=x+y$
Subject to the constraint,
$6 x+10 y \leq 500$
$\frac{x}{40}+\frac{y}{50} \leq 1$
$x, y \geq 0$
Now plotting both the line on graph paper, we have,
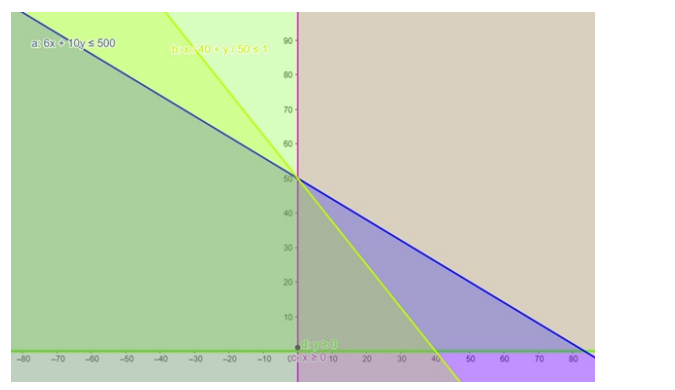
Distance covered with speed $40 \mathrm{~km} / \mathrm{hr}=\mathrm{x}=0$
Distance covered with speed $50 \mathrm{~km} / \mathrm{hr}=\mathrm{y}=50$
Therefore, maximum distance covered $=0+50=50 \mathrm{~km}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
