Question:
If $\mathrm{ABC}$ is a right triangle right-angled at $\mathrm{B}$ and $\mathrm{M}, \mathrm{N}$ are the mid-points of $\mathrm{AB}$ and $\mathrm{BC}$ respectively, then $4\left(\mathrm{AN}^{2}+\mathrm{CM}^{2}\right)=$
(a) $4 \mathrm{AC}^{2}$
(b) $5 \mathrm{AC}^{2}$
(c) $54 \mathrm{AC} 2$
(d) $6 \mathrm{AC}^{2}$
Solution:
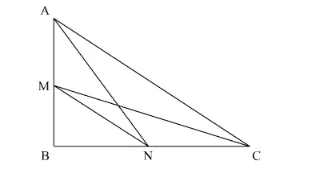
M is the mid-point of AB.
$\therefore B M=A B 2$
N is the mid-point of BC.
$\therefore B N=B C 2$
Now,
$A N^{2}+C M^{2}=\left(A B^{2}+\left(\frac{1}{2} B C\right)^{2}\right)+\left(\left(\frac{1}{2} A B\right)^{2}+B C^{2}\right)$
$=A B^{2}+\frac{1}{4} B C^{2}+\frac{1}{4} A B^{2}+B C^{2}$
$=\frac{5}{4}\left(A B^{2}+B C^{2}\right)$
$\Rightarrow 4\left(A N^{2}+C M^{2}\right)=5 A C^{2}$
Hence option (b) is correct.
