Question.
If $A D$ and $P M$ are medians of triangles $A B C$ and $P Q R$, respectively where $\Delta A B C \sim \Delta P Q R$, prove that $\frac{A B}{P Q}=\frac{A D}{P M}$.
If $A D$ and $P M$ are medians of triangles $A B C$ and $P Q R$, respectively where $\Delta A B C \sim \Delta P Q R$, prove that $\frac{A B}{P Q}=\frac{A D}{P M}$.
Solution:
$\Delta \mathrm{ABC} \sim \Delta \mathrm{PQR}$ (Given)
$\Rightarrow \frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A C}{P R}$
$\angle \mathrm{A}=\angle \mathrm{P}, \angle \mathrm{B}=\angle \mathrm{Q}, \angle \mathrm{C}=\angle \mathrm{R}$ ...(1)
Now, $\quad B D=C D=\frac{1}{2} B C$
and $\quad Q M=R M=\frac{1}{2} Q R$ ...(2)
( $\because \mathrm{D}$ is mid-point of $\mathrm{BC}$ and $\mathrm{M}$ is mid-point of $\mathrm{QR}$ )
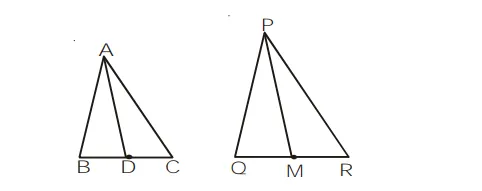
From (1), $\frac{A B}{P Q}=\frac{B C}{Q R} \Rightarrow \frac{A B}{P Q}=\frac{2 B D}{2 Q M}(B y(2))$
$\Rightarrow \frac{A B}{P Q}=\frac{B D}{Q M}$
Thus, we have $\frac{A B}{P Q}=\frac{B D}{O M}$
and $\angle \mathrm{ABD}=\angle \mathrm{PQM} \quad(\because \angle \mathrm{B}=\angle \mathrm{Q})$
$\Rightarrow \Delta \mathrm{ABD} \sim \Delta \mathrm{PQM} \quad$ (By SAS similarity criterion)
$\Rightarrow \frac{A B}{P Q}=\frac{A D}{P M}$
$\Delta \mathrm{ABC} \sim \Delta \mathrm{PQR}$ (Given)
$\Rightarrow \frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A C}{P R}$
$\angle \mathrm{A}=\angle \mathrm{P}, \angle \mathrm{B}=\angle \mathrm{Q}, \angle \mathrm{C}=\angle \mathrm{R}$ ...(1)
Now, $\quad B D=C D=\frac{1}{2} B C$
and $\quad Q M=R M=\frac{1}{2} Q R$ ...(2)
( $\because \mathrm{D}$ is mid-point of $\mathrm{BC}$ and $\mathrm{M}$ is mid-point of $\mathrm{QR}$ )

From (1), $\frac{A B}{P Q}=\frac{B C}{Q R} \Rightarrow \frac{A B}{P Q}=\frac{2 B D}{2 Q M}(B y(2))$
$\Rightarrow \frac{A B}{P Q}=\frac{B D}{Q M}$
Thus, we have $\frac{A B}{P Q}=\frac{B D}{O M}$
and $\angle \mathrm{ABD}=\angle \mathrm{PQM} \quad(\because \angle \mathrm{B}=\angle \mathrm{Q})$
$\Rightarrow \Delta \mathrm{ABD} \sim \Delta \mathrm{PQM} \quad$ (By SAS similarity criterion)
$\Rightarrow \frac{A B}{P Q}=\frac{A D}{P M}$
