If α and β are the zeros of a quadratic polynomial such that α + β = 24 and α − β = 8,

Given,

$\alpha+\beta=24 \ldots \ldots$ (i)

$\alpha-\beta=8 \ldots \ldots$ (ii)

By subtracting equation $(i i)$ from $(i)$ we get

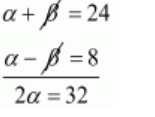
$\alpha=\frac{32}{2}$

$\alpha=16$

Substituting $\alpha=16$ in equation $(i)$ we get,

$\alpha+\beta=24$

$16+\beta=24$

$\beta=24-16$

$\beta=8$

Let S and P denote respectively the sum and product of zeros of the required polynomial. then, 

$S=\alpha+\beta$

$=16+8$

$=24$

$P=\alpha \beta$

$=16 \times 8$

$=128$

Hence, the required polynomial if $f(x)$ is given by

$f(x)=k\left(x^{2}-S x+P\right)$

$f(x)=k\left(x^{2}-24 x+128\right)$

Hence, required equation is $f(x)=k\left(x^{2}-24 x+128\right)$ where $k$ is any non-zeros real number.