If α and β are the zeros of the quadratic polynomial f(x)

(i) Since $\alpha$ and $\beta$ are the zeros of the quadratic polynomial $f(x)=x^{2}-2 x+3$

$\alpha+\beta=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$

$=\frac{-(-2)}{1}$

= 2

Product of the zeros $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$

$=\frac{3}{1}$

= 3

Let $S$ and $P$ denote respectively the sums and product of the polynomial whose zeros $\alpha+2, \beta+2$

$S=(\alpha+2)+(\beta+2)$

$S=\alpha+\beta+2+2$

$S=2+2+2$

$S=6$

$P=(\alpha+2)+(\beta+2)$

$P=\alpha \beta+2 \beta+2 \alpha+4$

$P=\alpha \beta+2(\alpha+\beta)+4$

$P=3+2(2)+4$

$P=3+4+4$

$P=11$

Therefore the required polynomial f (x) is given by 

$f(x)=k\left(x^{2}-S x+P\right)$

$=k\left(x^{2}-6 x+11\right)$

Hence, the required equation is $f(x)=k\left(x^{2}-6 x+11\right)$.

(ii) Since $\alpha$ and $\beta$ are the zeros of the quadratic polynomial $f(x)=x^{2}-2 x+3$

$\alpha+\beta=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$

$=\frac{-(-2)}{1}$

= 2

Product of the zeros $=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$

$=\frac{3}{1}$

= 3

Let $S$ and $P$ denote respectively the sums and product of the polynomial whose zeros $\frac{\alpha-1}{\alpha+1}, \frac{\beta-1}{\beta+1}$

$S=\frac{\alpha-1}{\alpha+1}+\frac{\beta-1}{\beta+1}$

$S=\frac{(\alpha-1)(\beta+1)+(\beta-1)(\alpha+1)}{(\alpha+1)(\beta+1)}$

$S=\frac{\alpha \beta-\beta+\alpha-1+\alpha \beta-\alpha+\beta-1}{\alpha \beta+\beta+\alpha+1}$

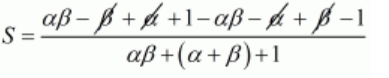
$S=\frac{\alpha \beta+\alpha \beta-1-1}{\alpha \beta+(\alpha+\beta)+1}$

By substituting $\alpha+\beta=2$ and $\alpha \beta=3$ we get,b

$S=\frac{3+3-1-1}{3+2+1}$

$S=\frac{6-2}{6}$

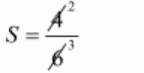
$P=\left(\frac{\alpha-1}{\alpha+1}\right)\left(\frac{\beta-1}{\beta+1}\right)$

$P=\frac{\alpha \beta-\beta-\alpha+1}{\alpha \beta+\beta+\alpha+1}$

$P=\frac{\alpha \beta-(\beta+\alpha)+1}{\alpha \beta+(\alpha+\beta)+1}$

$P=\frac{3-2+1}{3+2+1}$

$P=\frac{2}{6}$

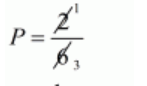
$P=\frac{1}{3}$

The required polynomial f (x) is given by,

$f(x)=k\left(x^{2}-S x+P\right)$

$f(x)=k\left(x^{2}-\frac{2}{3} x+\frac{1}{3}\right)$

Hence, the required equation is $f(x)=k\left(x^{2}-\frac{2}{3} x+\frac{1}{3}\right)$, where $k$ is any non zero real number.