If α and β are the zeros of the quadratic polynomial p(s)

Since $\alpha$ and $\beta$ are the zeros of the quadratic polynomial $p(s)=3 s^{2}-6 s+4$

$\alpha+\beta=\frac{-\text { Coefficient of } x}{\text { Coefficient of } x^{2}}$

$\alpha+\beta=\frac{-(-6)}{3}$

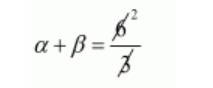
$\alpha+\beta=2$

$\alpha \beta=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}$

$\alpha \beta=\frac{4}{3}$

We have, $\frac{\alpha}{\beta}+\frac{\beta}{\alpha}+2\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)+3 \alpha \beta$

$=\frac{\alpha^{2}+\beta^{2}}{\alpha \beta}+2\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)+3 \alpha \beta$

By substituting $\alpha+\beta=2$ and $\alpha \beta=\frac{4}{3}$ we get,

$\frac{\alpha}{\beta}+\frac{\beta}{\alpha}+2\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)+3 \alpha \beta=\frac{(2)^{2}-2\left(\frac{4}{3}\right)}{\frac{4}{3}}+2 \frac{(2)}{\frac{4}{3}}+3\left(\frac{4}{3}\right)$

$\frac{\alpha}{\beta}+\frac{\beta}{\alpha}+2\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)+3 \alpha \beta=\frac{4-\frac{8}{3}}{\frac{4}{3}}+\frac{4}{\frac{4}{3}}+\frac{12}{3}$

$\frac{\alpha}{\beta}+\frac{\beta}{\alpha}+2\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)+3 \alpha \beta=\frac{\frac{4 \times 3}{1 \times 3}-\frac{8}{3}}{\frac{4}{3}}+\frac{4}{\frac{4}{3}}+\frac{12}{3}$

$\frac{\alpha}{\beta}+\frac{\beta}{\alpha}+2\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)+3 \alpha \beta=\frac{\frac{12-8}{3}}{\frac{4}{3}}+\frac{4}{\frac{4}{3}}+\frac{12}{3}$

$\frac{\alpha}{\beta}+\frac{\beta}{\alpha}+2\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)+3 \alpha \beta=\frac{\frac{4}{\frac{3}{4}}}{\frac{4}{3}}+\frac{4}{\frac{4}{3}}+\frac{12}{3}$

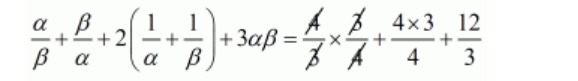
$\frac{\alpha}{\beta}+\frac{\beta}{\alpha}+2\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)+3 \alpha \beta=1+\frac{12}{4}+\frac{12}{3}$

$\frac{\alpha}{\beta}+\frac{\beta}{\alpha}+2\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)+3 \alpha \beta=\frac{1 \times 12}{1 \times 12}+\frac{12 \times 3}{4 \times 3}+\frac{12 \times 4}{3 \times 4}$

$\frac{\alpha}{\beta}+\frac{\beta}{\alpha}+2\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)+3 \alpha \beta=\frac{12+36+48}{12}$

$\frac{\alpha}{\beta}+\frac{\beta}{\alpha}+2\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)+3 \alpha \beta=\frac{48+48}{12}$

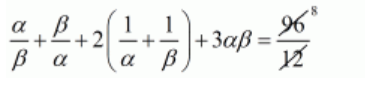
$\frac{\alpha}{\beta}+\frac{\beta}{\alpha}+2\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)+3 \alpha \beta=8$

Hence, the value of $\frac{\alpha}{\beta}+\frac{\beta}{\alpha}+2\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)+3 \alpha \beta$ is 8