If angle between two tangents drawn

True

From point $P$, two tangents are drawn.

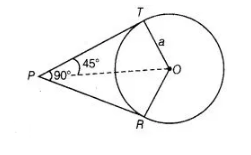
Given, $O T=a$

Also, line OP bisects the $\angle R P T$.

$\therefore$ $\angle T P O=\angle R P O=45^{\circ}$

Also, $O T \perp P T$

In right angied $\triangle O T P$. $\sin 45^{\circ}=\frac{O T}{O P}$

$\Rightarrow$ $\frac{1}{\sqrt{2}}=\frac{a}{O P} \Rightarrow O P=a \sqrt{2}$